计算二进制中1的个数

方法1：

利用取余的方式：用目标数对2取余，结果为1即1的个数加1

其原理其实就是将十进制化成二进制的过程，在过程中记录1的个数

源代码：

int fun1(int num){
	int count = 0;
	int temp;
	while(num){
		temp = num % 2;
		if(temp == 1)
			count ++;
		num /= 2;
	}
	return count;
}

方法2：该方法就是把十进制数看成二进制数计算，其利用移位运算移动目标数，用与运算记录1的个数。

例如：0000 0111 & 0000 0001 = 0000 0001 目标数向右移动一位 0000 0011继续与 0000 0001进行与运算

int fun2(int num){
	int count = 0;
	
	while(num){
		count += num & 1;
		num = num >> 1;
	}
	return count;
}

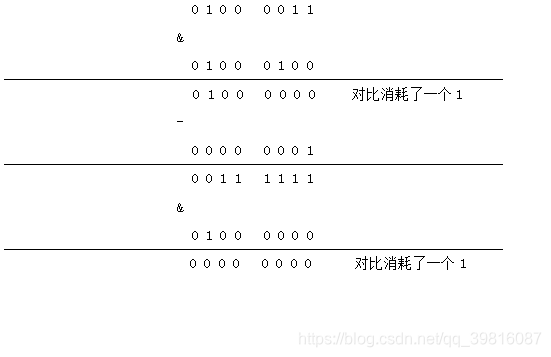
方法3：该方法旨在只扫描 1 的个数，利用位运算的逻辑，让其直接针对问题本身。想办法，用一个运算，使得每进行一次这样的运算就消耗一个1，使得算法的性能直接和二进制1的个数有关。我们知道，不管是什么进制的减运算，过程中，总会产生低位不足向高位借取的情况，而二进制的的减运算中，其结果不是1就是0。要使只消耗一个1，则用目标数减去1。而进位过后，与原来的数就会相异。相异的两个数，使用与运算，就会消走。

例如：0100 0111 要是每进行一次运算，就消耗一个1，其过程如下：

int fun3(int num){
	int count = 0;
	while(num){
		num &= (num -1);
       // example: 0100 0000 要使 1 -> 0 ,0011 1111 & 0100 0000 = 0000 0000 ，
      //0011 1111 = 0100 0000 - 0000 0001 
		count ++;// 始终要消耗一个 1 ，因为减 0000 0001，消耗的是最近的 1 
	}
	return count;
}

总结：

        在对一个问题的优化过程中，要慢慢的把解决方案直对问题本身，方法1 和方法2 中，其本身也很好的解决了问题，但在其运行的过程中，除了找到二进制中1的个数外（问题本身），还对0进行了扫描，此类扫描是多余的；而方法三就很好的解决了不用扫描二进制目标数中的0，直接记录其1的个数。该问题是个优化类的好问题。

欢迎转载，转载请注明出处！！！！！谢谢