《Hands-On Machine Learning with Scikit-Learn and TensorFlow》学习笔记第五篇----正则线性模型

最新推荐文章于 2025-02-02 23:37:02 发布

努力努力再努力F_

最新推荐文章于 2025-02-02 23:37:02 发布

阅读量180

点赞数

CC 4.0 BY-SA版权

分类专栏：机器学习笔记

本文链接：https://blog.youkuaiyun.com/qq_39751437/article/details/93381150

机器学习笔记专栏收录该内容

5 篇文章

订阅专栏

这篇学习笔记介绍了正则化线性模型，包括岭回归、套索回归和弹性网络。岭回归通过添加L2范数正则项来防止过拟合；套索回归利用L1范数实现特征选择，产生稀疏模型；弹性网络结合了岭回归和套索回归的优点，适用于相关特征场景。此外，还提到了早期停止法作为另一种正则化策略，并给出了选择模型的建议。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

对线性模型来说，正则化通常通过约束模型的权重来实现。接下来我们将会使用岭回归（Ridge Regression）、套索回归（LassoRegression）及弹性网络（Elastic Net）这三种不同的实现方法对权重进行约束。

一、岭回归（Ridge Regression）

岭回归（也叫作吉洪诺夫正则化）是线性回归的正则化版：在成本函数中添加一个等于的正则项。这使得学习中的算法不仅需要拟合数据，同时还要让模型权重保持最小。注意，正则项只能在训练的时候添加到成本函数中，一旦训练完成，你需要使用未经正则化的性能指标来评估模型性能。

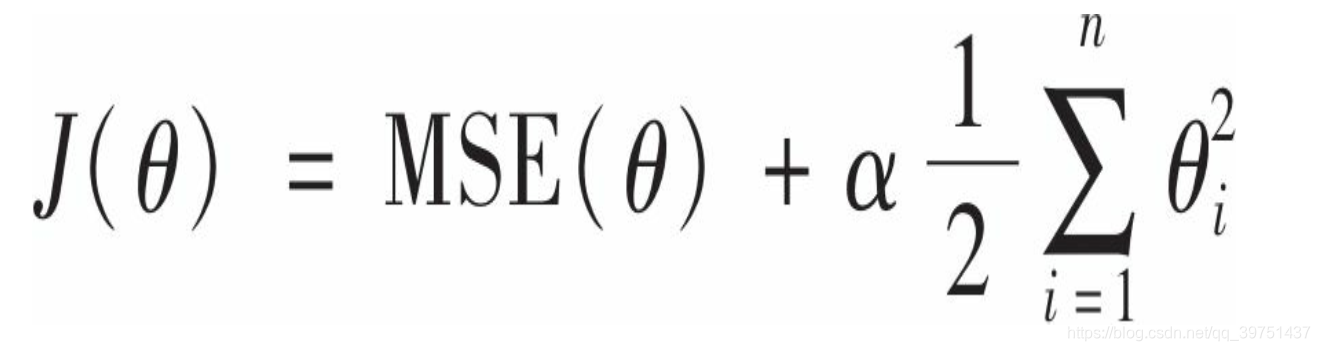
在这里插入图片描述
超参数α控制的是对模型进行正则化的程度。如果α=0，则岭回归就是线性模型。如果α非常大，那么所有的权重都将非常接近于零，这里偏置项 $θ_0$ 没有正则化。如果我们将w定义为特征权重的向量（ $θ_1$ 到 $θ_n$ ），那么正则项即等于1/2（ $w||^2$ ） 2其中 $w||^2$ 为权重向量的 $l_2$ 范数，所以岭回归相当于在成本函数上加了一个正则项（权重向量的 $l_2$ 范数）
要点：
在执行岭回归之前，必须对数据进行缩放（例如使用StandardScaler），因为它对输入特征的大小非常敏感，大多数正则化模型都是如此
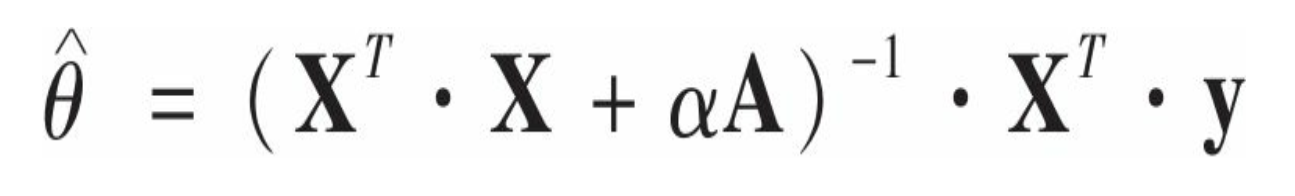
在这里插入图片描述
使用Scikit-Learn执行闭式解的岭回归，利用André-Louis Cholesky的矩阵因式分解法

from sklearn.linear_model import Ridge
from sklearn import datasets
iris=datasets.load_iris()
x=iris.data
y=iris.target
ridge_reg = Ridge(alpha=1, solver="cholesky")
ridge_reg.fit(x, y)
print (ridge_reg.predict([[4.6, 3.1, 1.5, 0.2]]))

二、套索回归

线性回归的另一种正则化，叫作最小绝对收缩和选择算子回归（Least Absolute Shrinkage and Selection Operator Regression，简称Lasso回归，或套索回归）。与岭回归一样， 它也是向成本函数增加一个正则项，但是它增加的是权重向量的 $l_1$ 范数
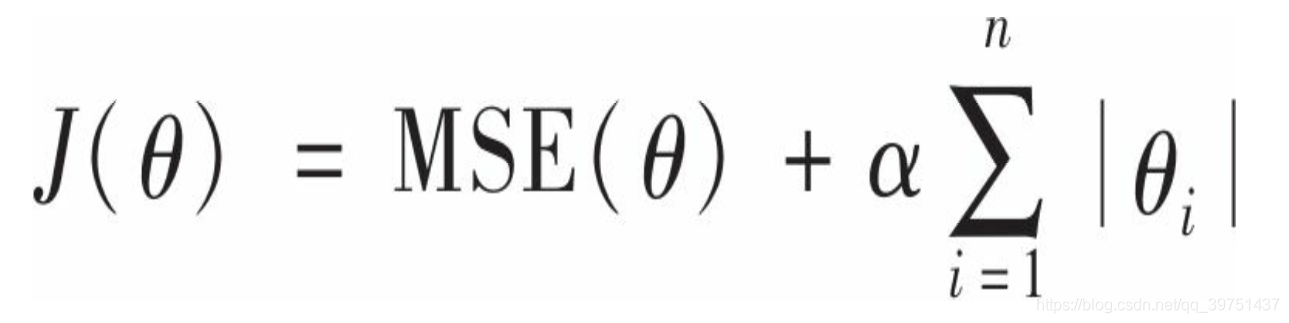
在这里插入图片描述
Lasso回归的一个重要特点是它倾向于完全消除掉最不重要特征的权重（也就是将它们设置为零）,Lasso回归会自动执行特征选择并输出一个稀疏模型（即只有很少的特征有非零权重）

from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(x, y)
print (lasso_reg.predict([[4.6, 3.1, 1.5, 0.2]]))

三、弹性网络

弹性网络是岭回归与Lasso回归之间的中间地带。其正则项就是岭回归和Lasso回归的正则项的混合，混合比例通过r来控制。当r＝0时，弹性网络即等同于岭回归，而当r＝1时，即相当于Lasso回归
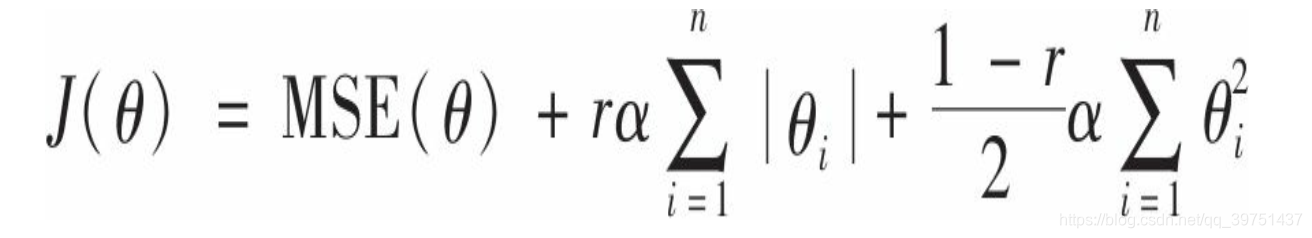
在这里插入图片描述
使用Scikit-Learn的ElasticNet的小例子（ $l_1$ _ratio对应混合比例 r）

from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(x, y)
print (elastic_net.predict([[4.6, 3.1, 1.5, 0.2]]))

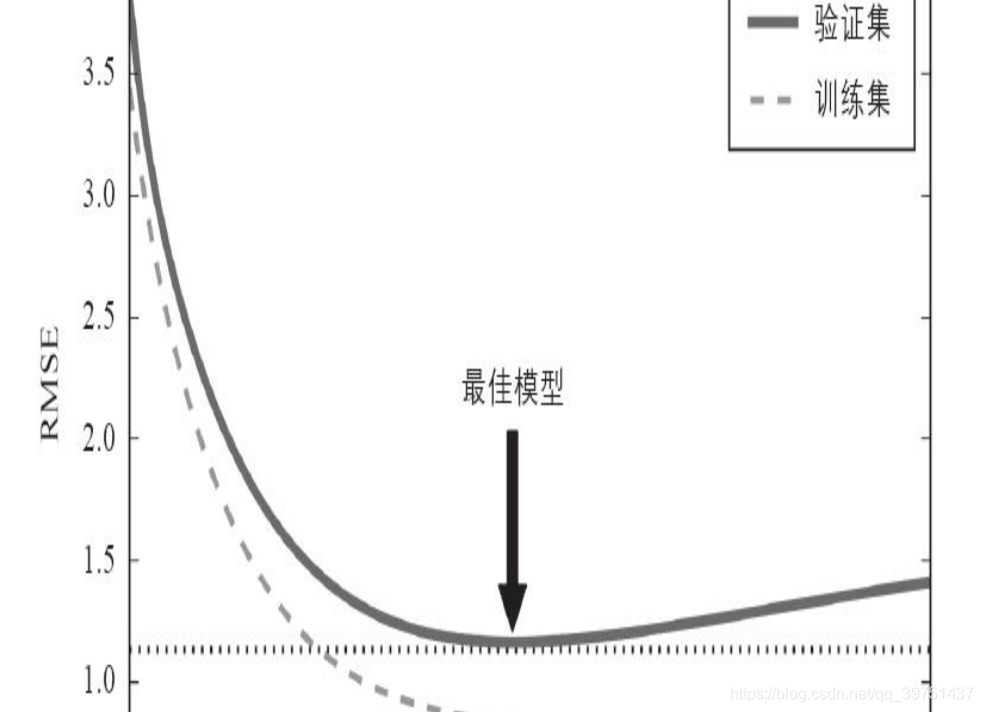
四、早期停止法

对于梯度下降这一类迭代学习的算法，还有一个与众不同的正则
化方法，就是在验证误差达到最小值时停止训练，该方法叫作早期停
止法
在这里插入图片描述

五、如何选择

有正则化的模型通常比没有正则化的模型表现得更好，所以应该优先选择岭回归而不是普通的线性回归。
Lasso回归使用1惩罚函数，往往倾向于将不重要的特征权重降至零。这将生成一个除了最重要的权重之外，其他所有权重都为零的稀疏模型。这是自动执行特征选择的一种方法，如果你觉得只有少数几个特征是真正重要的，这不失为一个非常好的选择，但是当您不确定的时候，应该更青睐岭回归模型。
·弹性网络比Lasso更受欢迎，因为某些情况下Lasso可能产生异常表现（例如当多个特征强相关，或者特征数量比训练实例多时）。并且，弹性网络会添加一个额外的超参数来对模型进行调整。如果你想使用Lasso，只需要将弹性网络的 $l_1$ _ratio设置为接近1即可