排序算法总结（JavaScript）

正文

---

排序算法说明

（1）排序的定义：对一序列对象根据某个关键字进行排序；
输入：n个数：a1,a2,a3,…,an
输出：n个数的排列:a1’,a2’,a3’,…,an’，使得a1’<=a2’<=a3’<=…<=an’。
再讲的形象点就是排排坐，调座位，高的站在后面，矮的站在前面咯。

（2）对于评述算法优劣术语的说明
稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；
不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；
内排序：所有排序操作都在内存中完成；
外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；
时间复杂度: 一个算法执行所耗费的时间。
空间复杂度: 运行完一个程序所需内存的大小。

（3）排序算法图片总结(图片来源于网络):

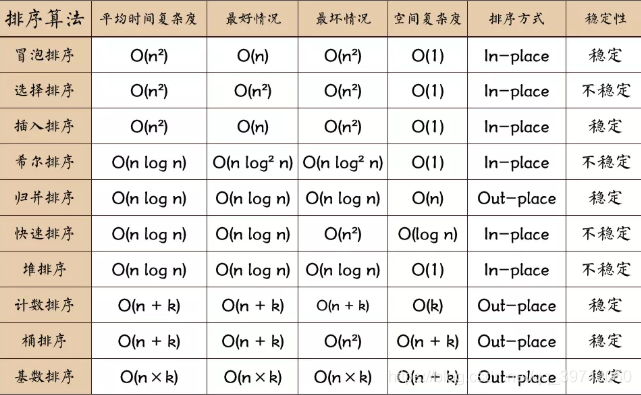
排序分类：

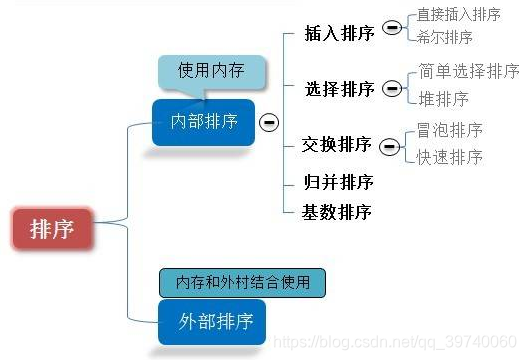
1.冒泡排序（Bubble Sort）

(1)算法描述

冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

(2)算法描述和实现

具体算法描述如下：

1. 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
3. 针对所有的元素重复以上的步骤，除了最后一个；
4. 重复步骤1~3，直到排序完成

JavaScript代码实现：

function bubbleSort(arr) {
    var len = arr.length;
    for (var i = 0; i < len; i++) {
        for (var j = 0; j < len - 1 - i; j++) {
            if (arr[j] > arr[j+1]) {        //相邻元素两两对比
                var temp = arr[j+1];        //元素交换
                arr[j+1] = arr[j];
                arr[j] = temp;
            }
        }
    }
    return arr;
}
var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];
console.log(bubbleSort(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

冒泡排序动图演示:

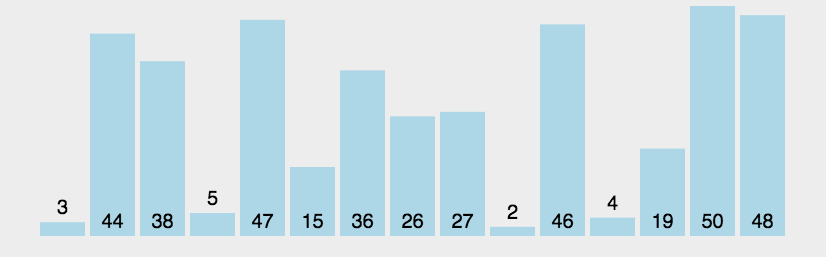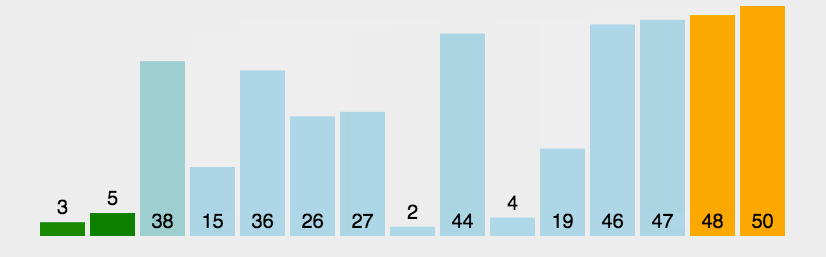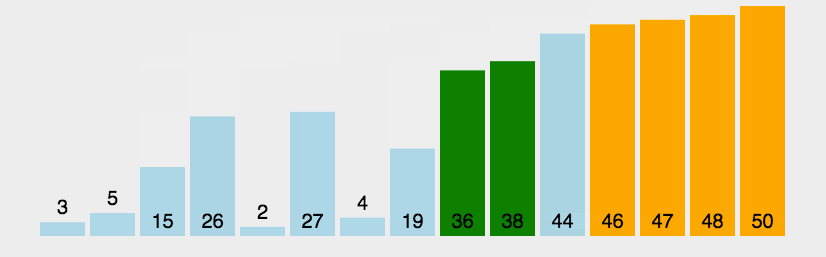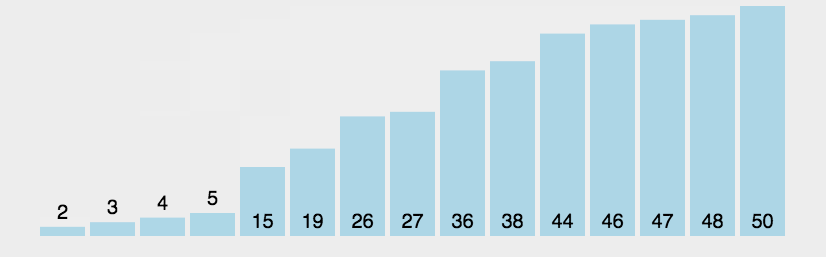
(3)算法分析

最佳情况：T(n) = O(n)
最差情况：T(n) = O(n2)
平均情况：T(n) = O(n2)

2.选择排序（Selection Sort）

(1)算法简介

选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

(2)算法描述和实现

n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下：

1. 初始状态：无序区为R[1…n]，有序区为空；
2. 第i趟排序(i=1,2,3…n-1)开始时，当前有序区和无序区分别为R[1…i-1]和R(i…n）。该趟排序从当前无序区中-选出关键字最小的记录 R[k]，将它与无序区的第1个记录R交换，使R[1…i]和R[i+1…n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区；
3. n-1趟结束，数组有序化了。

Javascript代码实现:

function selectionSort(arr) {
    var len = arr.length;
    var minIndex, temp;
    console.time('选择排序耗时');
    for (var i = 0; i < len - 1; i++) {
        minIndex = i;
        for (var j = i + 1; j < len; j++) {
            if (arr[j] < arr[minIndex]) {     //寻找最小的数
                minIndex = j;                 //将最小数的索引保存
            }
        }
        temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    console.timeEnd('选择排序耗时');
    return arr;
}
var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];
console.log(selectionSort(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

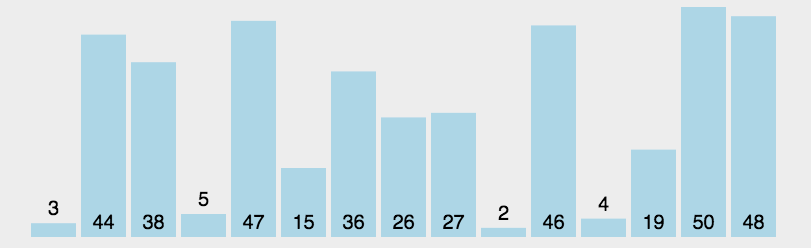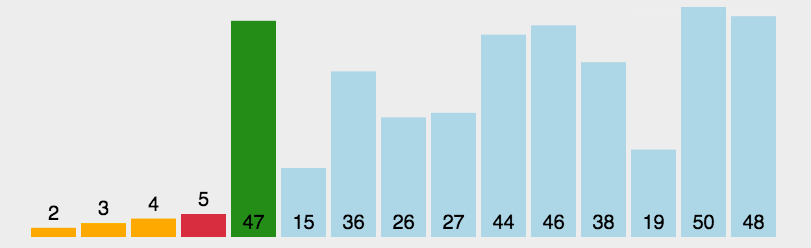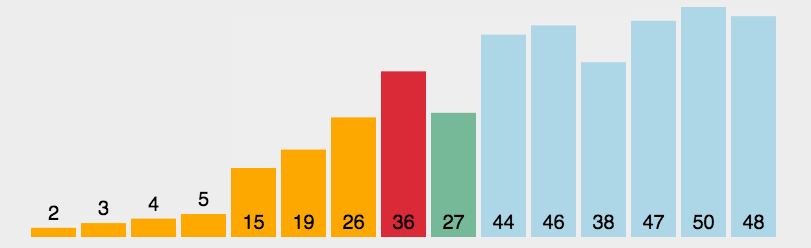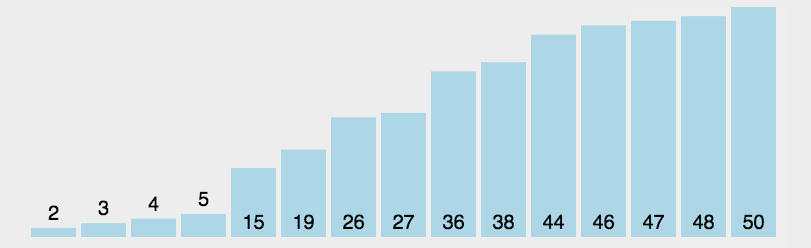
(3)算法分析

最佳情况：T(n) = O(n2)
最差情况：T(n) = O(n2)
平均情况：T(n) = O(n2)

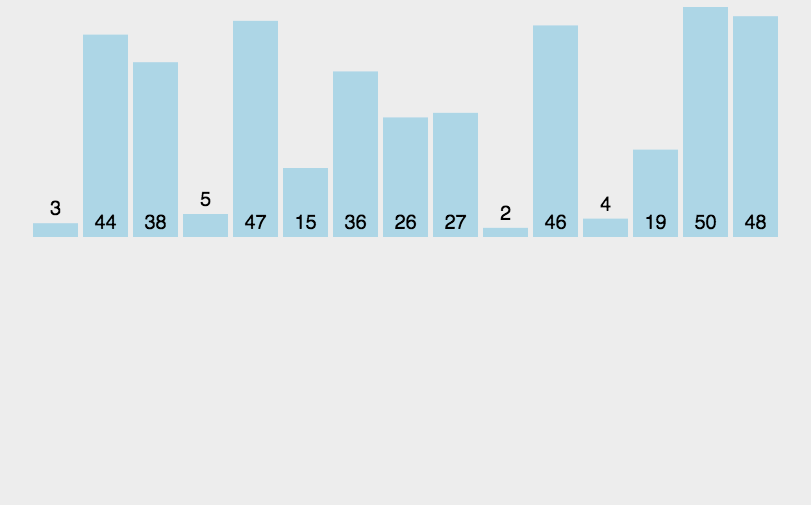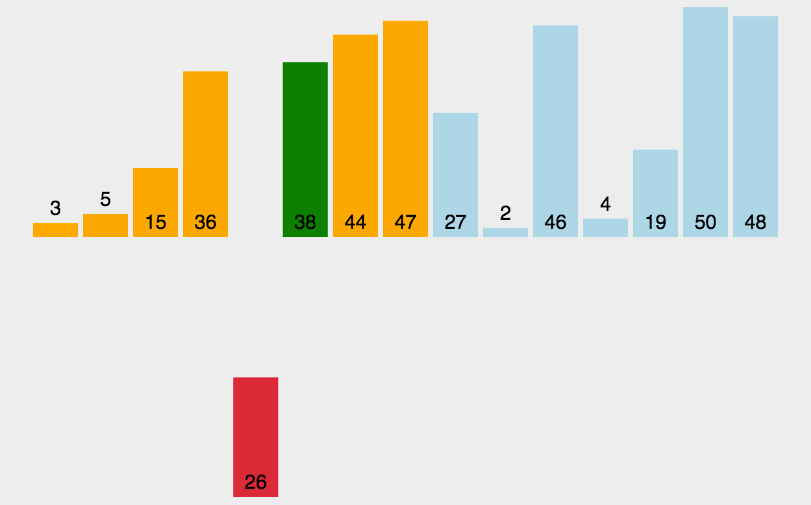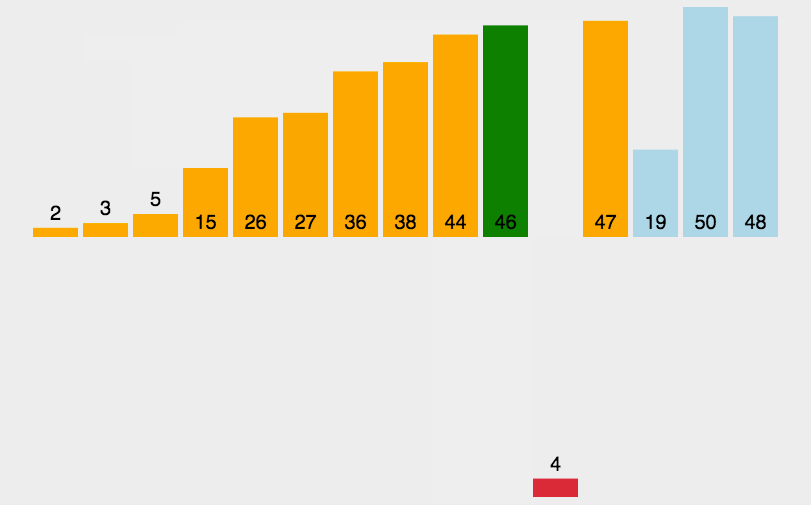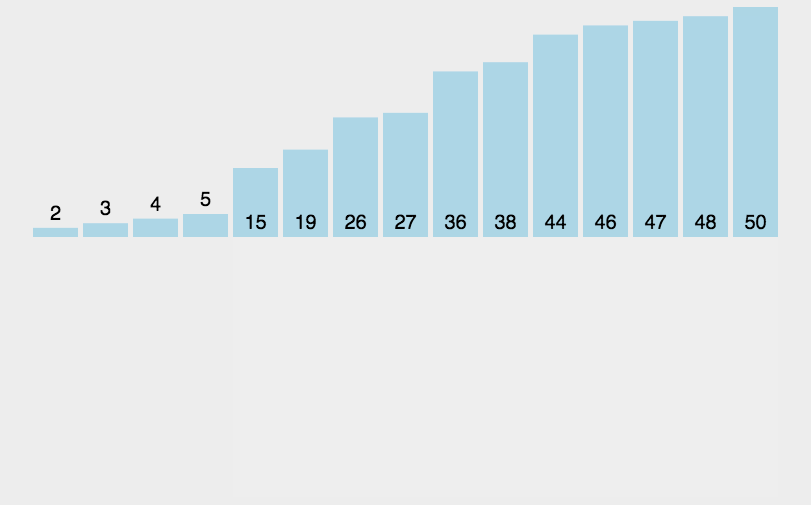
3.插入排序（Insertion Sort）

(1)算法简介

插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

(2)算法描述和实现：

一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

1. 从第一个元素开始，该元素可以认为已经被排序；
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描；
3. 如果该元素（已排序）大于新元素，将该元素移到下一位置；
4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
5. 将新元素插入到该位置后；
6. 重复步骤2~5。

Javascript代码实现:

function insertionSort(array) {
    if (Object.prototype.toString.call(array).slice(8, -1) === 'Array') {
        console.time('插入排序耗时：');
        for (var i = 1; i < array.length; i++) {
            var key = array[i];
            var j = i - 1;
            while (j >= 0 && array[j] > key) {
                array[j + 1] = array[j];
                j--;
            }
            array[j + 1] = key;
        }
        console.timeEnd('插入排序耗时：');
        return array;
    } else {
        return 'array is not an Array!';
    }
}

(3)算法分析

最佳情况：输入数组按升序排列。T(n) = O(n)
最坏情况：输入数组按降序排列。T(n) = O(n2)
平均情况：T(n) = O(n2)

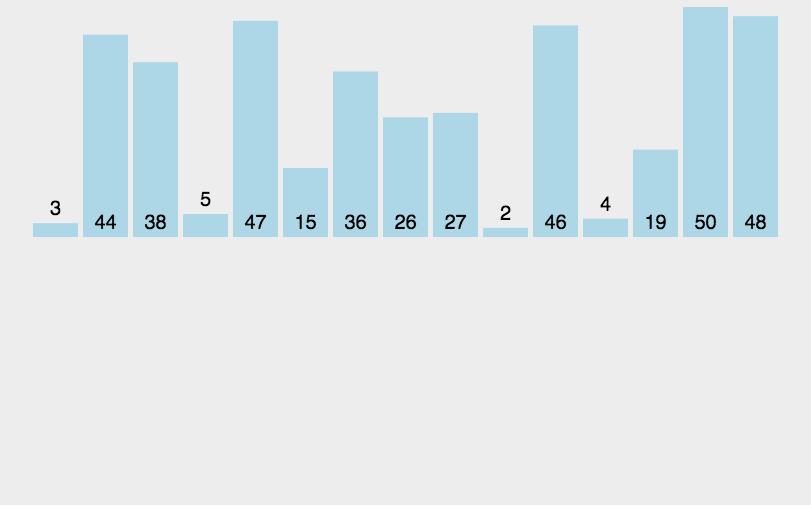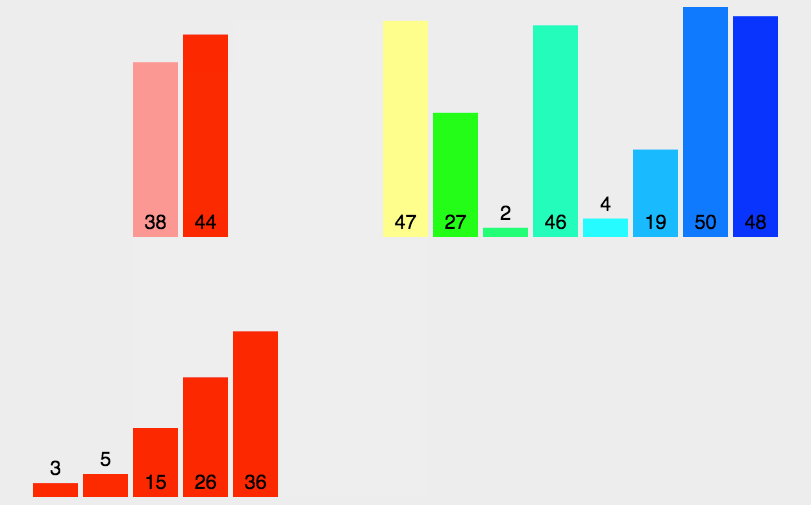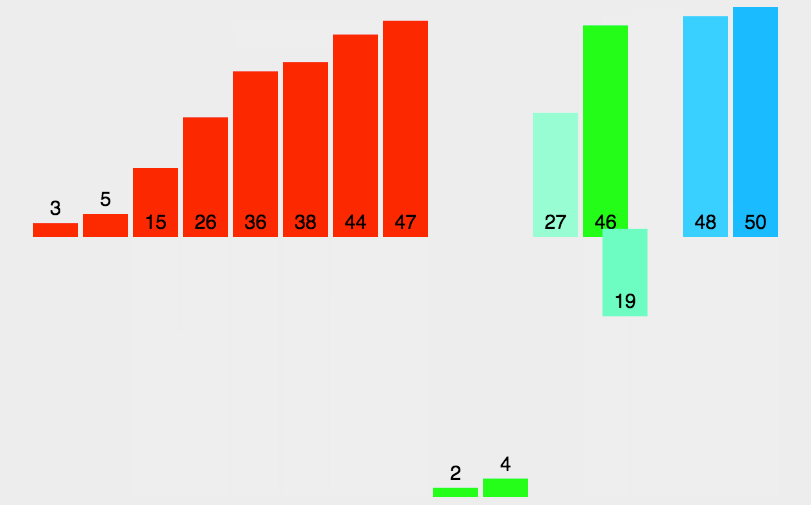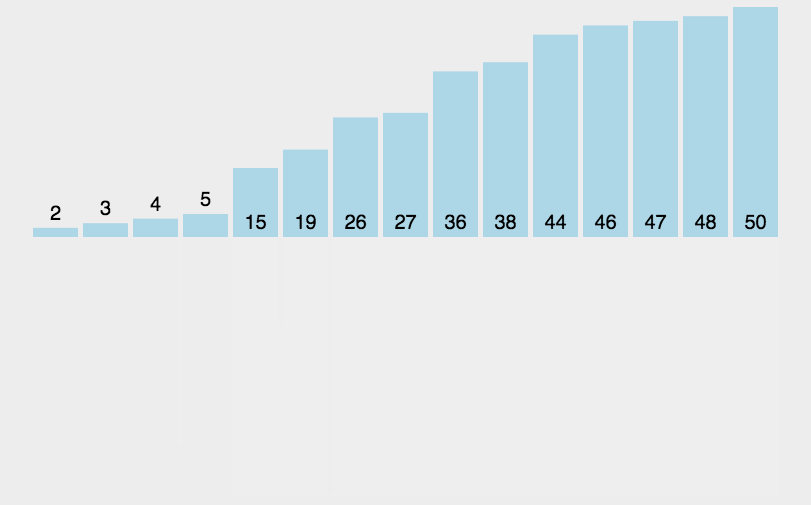
4.归并排序（Merge Sort）

(1)算法简介

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

(2)算法描述和实现：

具体算法描述如下：

1. 把长度为n的输入序列分成两个长度为n/2的子序列；
2. 对这两个子序列分别采用归并排序；
3. 将两个排序好的子序列合并成一个最终的排序序列。

Javscript代码实现:

function mergeSort(arr) {  //采用自上而下的递归方法
    var len = arr.length;
    if(len < 2) {
        return arr;
    }
    var middle = Math.floor(len / 2),
        left = arr.slice(0, middle),
        right = arr.slice(middle);
    return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right)
{
    var result = [];
    console.time('归并排序耗时');
    while (left.length && right.length) {
        if (left[0] <= right[0]) {
            result.push(left.shift());
        } else {
            result.push(right.shift());
        }
    }

    while (left.length)
        result.push(left.shift());

    while (right.length)
        result.push(right.shift());
    console.timeEnd('归并排序耗时');
    return result;
}
var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];
console.log(mergeSort(arr));

(3)算法分析

最佳情况：T(n) = O(n)
最差情况：T(n) = O(nlogn)
平均情况：T(n) = O(nlogn)

参考文章：https://juejin.im/post/57dcd394a22b9d00610c5ec8