EAGLE-2：通过动态草稿树加速语言模型推理

原创已于 2025-08-05 12:12:52 修改 · 872 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#语言模型 #人工智能 #自然语言处理

于 2025-08-05 12:11:49 首次发布

模型加速专栏收录该内容

16 篇文章

订阅专栏

温馨提示：
本篇文章已同步至"AI专题精讲" EAGLE-2：通过动态草稿树加速语言模型推理

摘要

现代 Large Language Models（LLMs）的推理过程既昂贵又耗时，而 speculative sampling 已被证明是一种有效的解决方案。大多数 speculative sampling 方法（例如 EAGLE）使用静态的 draft tree，并默认 draft token 的接受率仅依赖于其位置。有趣的是，我们发现 draft token 的接受率也依赖于上下文。本文在 EAGLE 的基础上提出了 EAGLE-2，该方法引入了一种新的 上下文感知动态 draft tree 技术用于 draft 建模。该改进利用了 EAGLE 的 draft 模型良好校准的特点：draft 模型的置信得分可以以较小误差逼近 token 的接受率。我们在三个系列的 LLM 和六个任务上进行了广泛评估，EAGLE-2 达到 3.05× 到 4.26× 的加速比，比 EAGLE-1 快 20%-40%。EAGLE-2 同时确保生成文本的分布保持不变，因此是一种 无损加速算法。

1. 引言

现代 Large Language Models（LLMs）（OpenAI, 2023；Touvron 等，2023）展现出了惊人的能力，并被广泛应用于各类场景。然而，其参数规模已大幅增长，甚至超过千亿。在自回归生成过程中，每生成一个 token 都需要访问全部模型参数。一次对话中可能会生成数百到数千个 token，这使得 LLM 推理过程既慢又昂贵Speculative sampling方法（Leviathan 等，2023；Chen 等，2023a）旨在解决这一问题，其核心思想是快速生成一批 draft token，并并行验证这些 token。通过在单次前向传播中生成多个 token，这些方法显著减少了推理延迟。
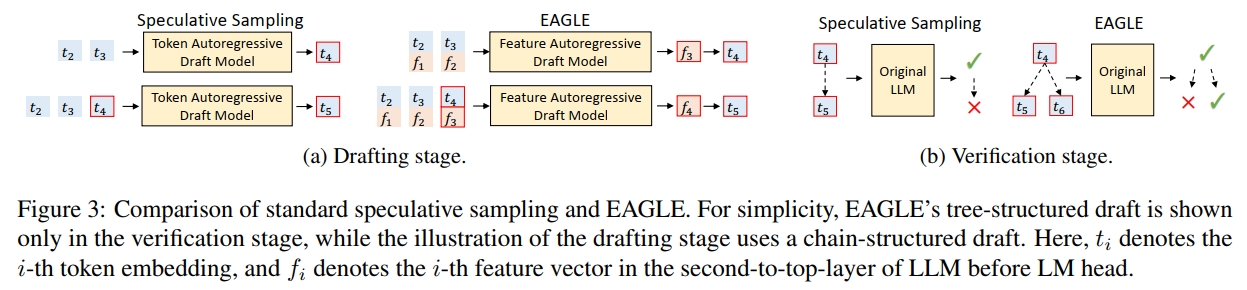
在这里插入图片描述

标准的 speculative sampling 方法（Leviathan et al., 2023；Chen et al., 2023a）使用链式结构的 draft。为了提高被接受的 token 序列长度，近期的 speculative sampling 工作引入了树状结构的 draft。Sequoia（Chen et al., 2024）显式地假设 draft token 的接受率仅依赖于其在树中的位置。EAGLE（Li et al., 2024b）和 Medusa（Cai et al., 2024）在所有上下文中使用相同的静态 draft tree 结构：在 draft 阶段的第 i 步，添加 k 个候选 token，且 k 为固定值。这种做法隐含地采纳了上述假设。然而，这一假设似乎与 speculative sampling 的基本直觉相矛盾：某些 token 更容易预测，较小的模型就能准确地预测它们。我们的实验（见第 3.1 节）表明，draft token 的接受率不仅依赖于其位置，还高度依赖于上下文。因此，静态 draft tree 结构存在内在的局限性。根据不同上下文中 draft token 的接受率动态调整 draft tree 的结构，能够取得更好的效果。
在这里插入图片描述
然而，获取 draft token 的接受率需要原始 LLM 的前向计算结果，这与 speculative sampling 减少原始 LLM 前向调用次数的目标相冲突。幸运的是，我们发现 EAGLE 的置信度校准效果良好：draft 模型的置信分数（即概率）可以很好地近似 draft token 的接受率（见第 3.2 节）。这使得基于上下文的动态 draft tree 结构成为可行的选择。

我们提出 EAGLE-2，该方法利用 draft 模型的置信分数来近似接受率。在此基础上，它动态调整 draft tree 的结构，从而提升被接受的 token 数量。我们在六个任务上进行了全面且广泛的测试：多轮对话、代码生成、数学推理、指令跟随、文本摘要以及问答任务。所使用的数据集包括：MT-bench（Zheng et al., 2023）、HumanEval（Chen et al., 2021）、GSM8K（Cobbe et al., 2021）、Alpaca（Taori et al., 2023）、CNN/Daily Mail（Nallapati et al., 2016）以及 Natural Questions（Kwiatkowski et al., 2019）。对比方法涵盖了六种先进的 speculative sampling 技术：标准 speculative sampling（Leviathan et al., 2023；Chen et al., 2023a；Joao Gante, 2023）、PLD（Saxena, 2023）、Medusa（Cai et al., 2024）、Lookahead（Fu et al., 2023）、Hydra（Ankner et al., 2024）以及 EAGLE（Li et al., 2024b）。实验基于三类 LLM 系列：Vicuna、LLaMA2-Chat 和 LLaMA3-Instruct。

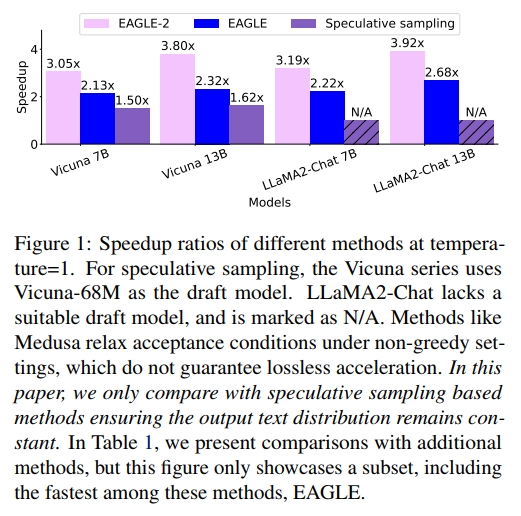
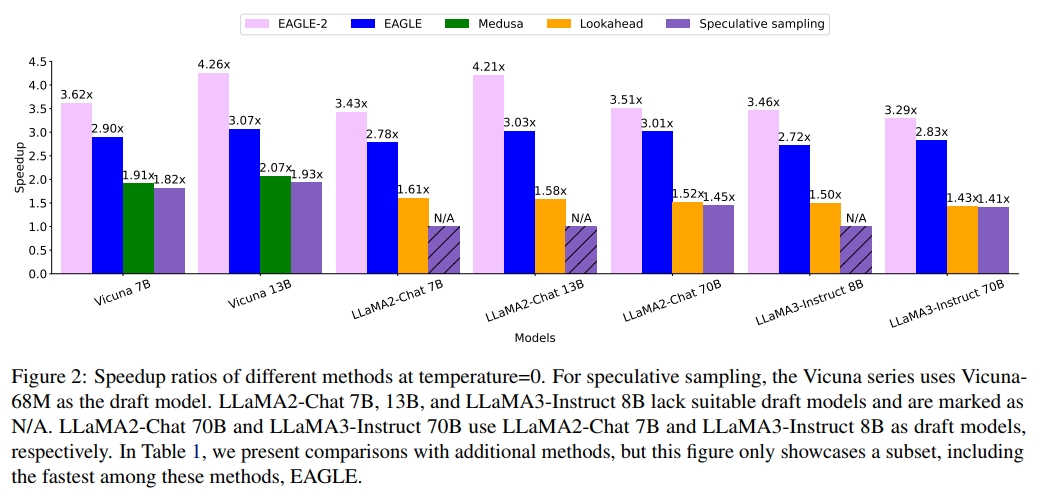
在所有实验中，EAGLE-2 表现最佳，取得了 2.5 倍到 5 倍的加速效果。图 1 和图 2 展示了 EAGLE-2 与其他 speculative sampling 方法在 MT-bench 上的加速比。MT-bench 是一个多轮对话数据集，非常贴近 ChatGPT 等模型的真实应用场景，并被广泛用于评估最先进的开源或闭源模型。在 MT-bench 数据集上，EAGLE-2 的速度大约是 Medusa 的 2 倍，约为 Lookahead 的 2.3 倍，同时确保输出分布保持不变。

除了性能表现之外，EAGLE-2 还具有以下优势：

开箱即用。相比 EAGLE，EAGLE-2 无需训练任何额外的模型。它不需要训练一个单独的模型来预测 draft tree 结构，而是基于 draft 模型的置信分数动态调整 draft tree 结构，这一点对于 speculative sampling 至关重要。因此，EAGLE-2 完全无需额外训练。
可靠性。EAGLE-2 不对原始 LLM 的参数进行微调或更新，也不会放宽 token 的接受条件。这确保了生成文本的分布与原始 LLM 完全一致，并且在理论上是可证的。

2. 预备知识

2.1. 推测式采样

Speculative sampling（Leviathan 等，2023；Chen 等，2023a；Sun 等，2024c；2024b）的核心思想是“先起草，后验证”：先快速生成一个可能正确的草稿，然后检查草稿中哪些 token 是可以接受的。我们用 $t_i$ 表示第 i 个 token，用 $T_{a:b}$ 表示从$ t_a$ 到 $t_b$ 的 token 序列，即 $t_a, t_{a+1}, ···, t_b$ 。Speculative sampling 在草稿生成阶段与验证阶段之间交替进行。
在这里插入图片描述

设有前缀 $T_{1:j}$ ，在草稿生成阶段，speculative sampling 使用一个草稿模型（比原始 LLM 更小的模型）以 $T_{1:j}$ 为前缀，自回归地生成一个草稿序列 $\hat{T}_{j+1:j+k}$ ，同时记录每个 token 的概率 $\hat{p}$ 。

在验证阶段，speculative sampling 调用原始 LLM 来检查草稿 $\hat{T}_{j+1:j+k}$ ，并记录其对应的概率 $p$ 。然后，speculative sampling 从前往后依次决定草稿中每个 token 的接受与否。对于第 $j + i$ 个草稿 token $\hat{t}_{j+i}$ ，它被接受的概率为： $\operatorname* { m i n } ( 1 , p _ { j + i } ( \hat { t } _ { j + i } ) / \hat { p } _ { j + i } ( \hat { t } _ { j + i } ) )$ ，如果该 token 被接受，则继续检查下一个；否则，从分布 $\text{norm}(\max(0, p_{j+i} - \hat{p}_{j+i}))$ 中重新采样一个 token 来替换 $\hat{t}_{j+i}$ ，并丢弃草稿中其后的所有 token。Leviathan 等（2023）在其附录 A.1 中证明了 speculative sampling 与标准自回归解码的分布是一致的。EAGLE 和 EAGLE-2 都遵循这一框架。

2.2 EAGLE

EAGLE（Li 等，2024b）是对 speculative sampling 的一种改进方法。在本工作提交时，EAGLE 在 Spec-Bench（Xia 等，2024）上排名第一。Spec-Bench 是一个为评估不同场景下的 speculative decoding 方法而设计的全面基准测试。

草稿生成阶段（Drafting Stage）
与标准的 speculative sampling 使用自回归方式预测 token 序列不同，EAGLE 在更结构化的特征层级（即在 LM Head 之前的特征层）上进行自回归生成，然后再使用原始 LLM 的 LM Head 获取草稿 token。
由于该采样过程会在特征序列中引入不确定性，为了解决这一问题，EAGLE 还向草稿模型输入一个提前一步的 token 序列，如图 3a 所示。

验证阶段（Verification Stage）
在标准的 speculative sampling 中，草稿结构是链式的（chain-structured），这意味着一旦某个草稿 token 被拒绝，其后所有 token 都必须被丢弃。而 EAGLE 使用树结构的草稿（tree-structured draft），当某个草稿 token 被拒绝时，可以尝试其它的备选分支。图 3b 展示了两者之间的区别。
在这里插入图片描述
EAGLE 与 EAGLE-2 的区别
EAGLE 的草稿树结构是固定的，在草稿生成阶段会填充对应的位置。EAGLE-2 的目标是在此基础上进一步改进，通过引入可动态调整的草稿树来增强生成能力。图 4 以一个简单的示例说明了 EAGLE 与 EAGLE-2 之间的差异。

3. 观察结果

3.1 依赖上下文的接受率

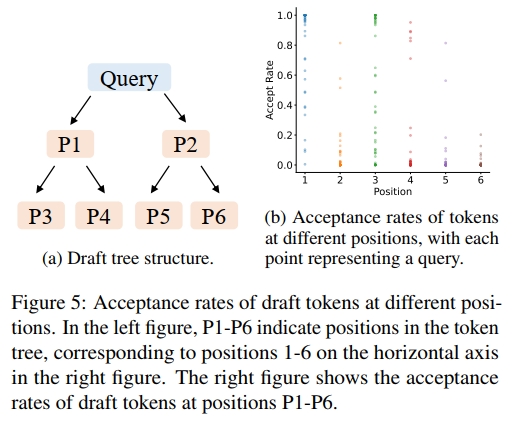
首先，我们评估了使用动态草稿树的必要性，这取决于草稿token的接受率是否仅与其在草稿树中的位置相关。我们在 Alpaca 数据集和 Vicuna 7B 模型上测试了不同位置的草稿token的接受率，结果如图 5 所示。总体来看，草稿token的接受率确实与位置有关：位置 P1 的接受率最高，位置 P6 的接受率最低。草稿树左上方（如位置 P1）的token接受率较高，而右下方（如位置 P6）的接受率较低。这也解释了为什么静态草稿树（如 EAGLE 和 Medusa 中使用的）在左上方节点较多、右下方节点较少的设计合理性。然而，我们还观察到相同位置的接受率存在显著差异，这表明草稿token被接受的概率不仅依赖位置，还与上下文有关。这提示我们，基于上下文的动态草稿树比静态草稿树具有更大的潜力。
在这里插入图片描述

3.2 草稿模型的良好校准性

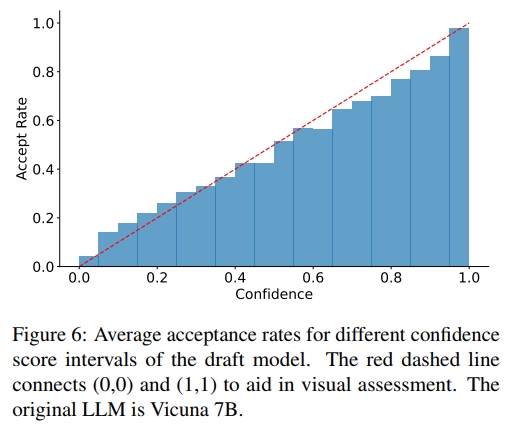
为了应用动态草稿树，我们需要一种低成本的方法来估计草稿令牌的接受率，而无需调用原始 LLM。我们在 Alpaca 数据集上进行了实验，探究草稿模型的置信度分数（即 LLM 对每个 token 输出的概率）与接受率之间的关系。如图 6 所示，草稿模型的置信度分数与令牌的接受率之间呈现出强正相关关系。例如，置信度分数低于 0.05 的草稿令牌，其接受率约为 0.04；而置信度分数高于 0.95 的令牌，其接受率约为 0.98。因此，我们可以使用草稿模型的置信度分数来估计接受率，无需额外开销，从而支持对草稿树的动态调整。在其他方法的草稿模型中，如 GLIDE 和 CAPE（Du 等人，2024），也观察到了类似的现象。

4. 基于上下文的动态草稿树

基于上述观察结果，我们提出 EAGLE-2，这是一种用于 LLM 推理加速的算法，它能够动态调整草稿树结构。EAGLE-2 不改变草稿模型的训练与推理过程，也不影响验证阶段，其改进主要体现在两个方面：如何扩展草稿树（见第 4.1 节）以及如何对草稿令牌重新排序（见第 4.2 节）。在扩展阶段，我们将当前草稿树最新一层中最有希望被接受的节点输入草稿模型，以生成下一层草稿令牌；在重新排序阶段，我们选择接受概率更高的令牌，作为传入原始 LLM 的验证输入。

在草稿树中，每个节点代表一个 token。下文中，“节点”和“token”将交替使用。
在这里插入图片描述

4.1 扩展阶段

得益于树状注意力机制（tree attention），草稿模型可以同时输入当前层的所有 token，并在一次前向传播中计算出下一步 token 的概率，从而实现对当前层所有 token 的扩展。然而，如果一次性输入太多 token，草稿模型的前向传播速度可能会下降；同时，草稿树每一层中的 token 数量会呈指数级增长。因此，我们需要对草稿树进行选择性扩展。

我们从当前层中选择全局接受概率最高的前 $k$ 个 token 进行扩展。在 speculative sampling 中，如果一个草稿 token 被拒绝，则其后所有 token 都会被丢弃；一个 token 只有在其所有前缀都被接受的情况下才最终被接受。因此，token $t_i$ 的全局接受率是从根节点到 $t_i$ 路径上所有 token 的接受率的乘积。我们将其定义为值 $V_i$ ：
$\prod _ { t _ { j } \in \mathrm { P a t h } ( \mathrm { r o o t } , t _ { i } ) } p _ { j } \approx \prod _ { t _ { j } \in \mathrm { P a t h } ( \mathrm { r o o t } , t _ { i } ) } c _ { j } ,$
其中，Path(root,  $t_{i}$ ) 表示从根节点到草稿树中节点  $t_{i}$ 的路径， $p_{j}$ 表示节点  $t_{j}$ 的接受率， $c_{j}$ 表示草稿模型对 $tⱼ $的置信度分数。第 3.2 节的实验表明，置信度分数与接受率之间存在显著的正相关关系。我们利用这一关系来近似估算该值。

从具有较高 V 值的 token 开始的分支更有可能被接受。因此，我们从最后一层中选择值最大的前 k 个节点作为草稿模型的输入，并根据其输出扩展草稿树。图 7 顶部展示了扩展阶段的流程。

4.2 重排序阶段

扩展阶段的目的是加深草稿树。由于接受率的取值范围在 0 到 1 之间，越深的 token，其值越低。一些未被扩展的浅层节点可能比已扩展的深层节点具有更高的值。因此，我们不会直接将扩展阶段选出的 token 作为最终草稿，而是对所有草稿 token 进行重排序，并选择值最高的前 m 个 token。一个节点的值始终小于或等于其父节点的值。对于值相同的节点，我们优先选择更浅层的节点。这样可以确保重排序后选出的前 m 个 token 仍然构成一棵连通的树。

随后，我们将这些被选中的 token 展平为一维序列，用作验证阶段的输入。为了确保与标准自回归解码保持一致，还需调整注意力掩码（attention mask）。在标准自回归解码中，每个 token 都可以看到其之前的所有 token，因此形成的是一个下三角的注意力矩阵。而在草稿树中，来自不同分支的 token 之间不应彼此可见，因此必须根据树的结构调整注意力掩码，确保每个 token 只能看到它的祖先节点。图 7 底部展示了重排序阶段的过程。

温馨提示：
阅读全文请访问"AI深语解构" EAGLE-2：通过动态草稿树加速语言模型推理