Python数据挖掘与分析-------多因子探索分析

最新推荐文章于 2025-05-19 23:12:32 发布

原创

最新推荐文章于 2025-05-19 23:12:32 发布 · 2.5k 阅读

·

0

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

#数据分析 #多因子探索分析

本文深入探讨Python中的数据挖掘与分析，包括假设检验（如卡方检验和方差分析）、相关系数（皮尔逊和斯皮尔曼）、线性回归及其决定系数、主成分分析（PCA）和交叉分析等统计方法，旨在理解变量间的关联及差异性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、假设检验与方差检验

①假设检验

1.建立原假设Ho（包含等号）,Ho的反命题为H1备择假设

2.选择检验统计量

假设检验量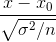： $\frac{x-x_{0}}{\sqrt{\sigma ^{2}/n}}$

3.根据显著水平，确定拒绝域（一般为0.05）与之相反的是接受域
4.计算P值或样本值做出判断

根据检验量，查【标准正态分布表】得到P值 ,得到的P值跟拒绝域做比较，判断假设条件是否成立。

②卡方检验

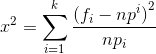
$x^{2}=\sum _{i=1}^{k}\frac{\left ( f_{i}-np^{i} \right )^{2}}{np_{i}}$

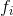$f_{i}$ 是实际的值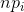， $np_{i}$ 是预测值

根据公式计算出卡方值。

然后根据拒绝域P值通过查表【分布临界值表】查出卡方值，对比求出的卡方值进行判断条件是否成立。

③方差检验

判断两组以上的样本均值是否有显著性差异

总平方和SST（total sum of squares）

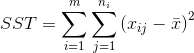
$SST=\sum_{i=1}^{m} \sum_{j=1}^{n_{i}}\left ( x_{ij} - \bar x \right )^{2}$

解释平方和SSE（explained sum of squares），也成模型平方和

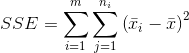
$SSE=\sum_{i=1}^{m} \sum_{j=1}^{n_{i}}\left ( \bar x_{i} -\bar x \right )^{2}$

残差平方和SSR（residual sum of squares），也称剩余平方和

最低0.47元/天解锁文章

200万优质内容无限畅学

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。