代码参考了知乎以及机器学习实战的内容,数据集为机器学习实战的testSet.txt
machine learning inaction - Ch05 - testSet.txt可自行在GitHub搜索获得,此处不提供了。
matlab代码
clear;
clc;
% 逻辑回归
path='E:\Codes\Python\ML\testSet.txt';
[data,label]=loadDataSet(path);
[m,n]=size(data);
alpha=0.001;
theta=ones(n,1);% 3*1
# 循环次数
Loop=10000;
for i=1:Loop
P = sigmoid(data*theta);
error=loss(P,label);
theta=update_theta(alpha,data,error,theta);
end
disp(theta);
% 绘图
%1. 描点,不同分类不同样式
path='E:\Codes\Python\ML\testSet.txt';
dataSet=importdata(path);
[m,n]=size(dataSet); % m*n
x1=[];y1=[];
x2=[];y2=[];
for i=1:m
if dataSet(i,3)==0
x1(end+1)=dataSet(i,1);
y1(end+1)=dataSet(i,2);
else
x2(end+1)=dataSet(i,1);
y2(end+1)=dataSet(i,2);
end
end
%2. 画线,一条直线分隔两类
xx1=-3.0;
yy1=(-theta(1)-theta(2)*xx1)/theta(3);
xx2=3.0;
yy2=(-theta(1)-theta(2)*xx2)/theta(3);
plot([xx1,yy1],[xx2,yy2]);
hold on
scatter(x1,y1,'k')
hold on
scatter(x2,y2,'r*')
%1. 生成dataMat与labelMat
function [dataMat,labelMat]=loadDataSet(path)
% dataMat shape为100*3,数据为[1, *, *]酱婶的
% labelMat shape为100*1,数据为testSet的第三列
testSet=importdata(path);
dataMat=ones(100,1);
Mat1=[1,0,0];
Mat2=[0,1,0;0,0,1;0,0,0];
dataMat=dataMat*Mat1+testSet*Mat2;
labelMat=testSet(:,3);
end
%2. sigmoid函数
function sig=sigmoid(input_x)
sig=1.0 ./ (1.0+exp(-input_x));
end
%3. 损失函数
function error=loss(P, y)
error=P-y;
end
%4. 更新权值
function theta=update_theta(alpha, X, error, theta)
grad=X'*error;
theta=theta-alpha*grad;
end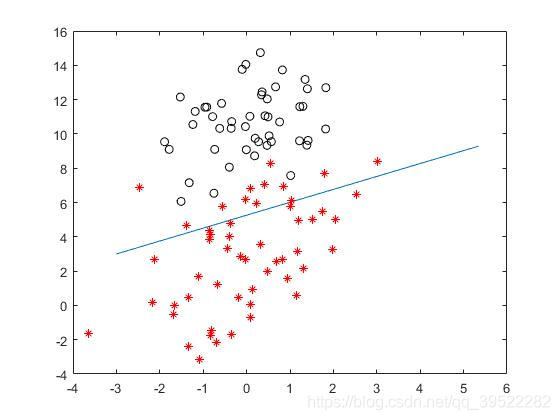
python 实现
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from numpy.linalg import inv
def loadDataSet(path):
dataMat = []
labelMat = []
fr = open(path)
for line in fr.readlines():
lineArr = line.strip().split() #根据空格切分原来的长字符串
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])#最开始的1.0是最后的常数项
labelMat.append(int(lineArr[2]))
fr.close()
return dataMat,labelMat
# sigmoid函数
def sigmoid(input_x):
return 1.0/(1.0+np.exp(-input_x))
# 损失函数
def loss(P, y):
return (P - y)
# 更新权值
def update_theta(alpha, X, error, theta):
grad = np.dot(X.T, error)
theta -= alpha * grad
return theta
# 保存记录目标函数的值,以便观察是否越接近损失theta
def save_cost(P, y, N):
j = -np.sum(y * np.log(P) + (1 - y) * np.log(1 - P))
return (1 / N) * j
def plotBestFit(theta):
n = np.shape(dataMat)[0] #数据个数
xcord1 = []; ycord1 = [] #第一类数据的坐标
xcord2 = []; ycord2 = [] #第二类数据的坐标
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataMat[i,1])
ycord1.append(dataMat[i,2])
else:
xcord2.append(dataMat[i,1])
ycord2.append(dataMat[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green', marker='*')
x = np.arange(-3.0, 3.0, 0.1)
y = (-theta[0] - theta[1]*x)/theta[2]
ax.plot(x, y)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
path='E:\\Codes\\Python\\ML\\testSet.txt'
dataMat, labelMat = loadDataSet(path)
m, n = np.shape(dataMat)
alpha = 0.001
theta = np.ones((n,1)) # 3*1
print(theta)
maxLoop = 300000
dataMat = np.array(dataMat)
labelMat = np.array(labelMat)[:,np.newaxis]
for i in range(maxLoop):
P = sigmoid(np.dot(dataMat, theta))
error = loss(P, labelMat)
theta = update_theta(alpha, dataMat, error, theta)
print("theta = ")
print(theta)
plotBestFit(theta)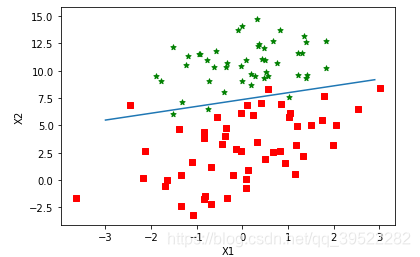








 本文探讨了逻辑回归的实现,分别使用MATLAB和Python两种编程语言进行演示。代码灵感来源于知乎和《机器学习实战》一书,使用的数据集为testSet.txt,可以在GitHub上自行获取。
本文探讨了逻辑回归的实现,分别使用MATLAB和Python两种编程语言进行演示。代码灵感来源于知乎和《机器学习实战》一书,使用的数据集为testSet.txt,可以在GitHub上自行获取。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








