LeetCode HOT 100 —— 437. 路径总和 III

题目

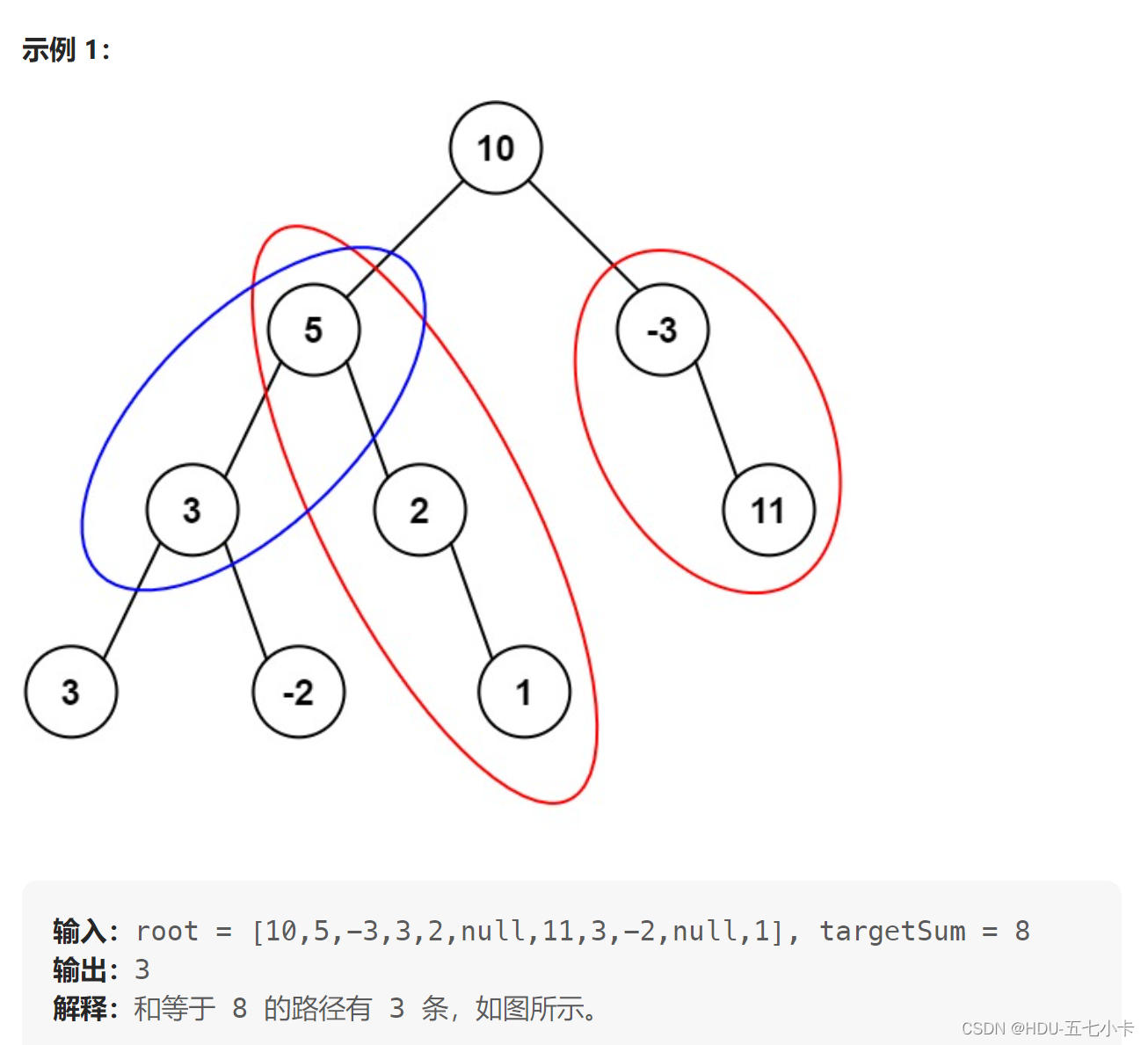
给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

思路

方法一：双重递归（牛）

思想：首先先序递归遍历每个节点，再以每个节点作为起始点递归寻找满足条件的路径。

java代码如下：

class Solution { 
    int pathnumber;
    public int pathSum(TreeNode root, long sum) {//因为力扣有个特别变态的测试用例，[1000000000,1000000000,null,294967296,null,1000000000,null,1000000000,null,1000000000],int会溢出报错，所以要用long
            if(root == null) return 0;   
            Sum(root,sum);
            pathSum(root.left,sum);
            pathSum(root.right,sum); 
            return pathnumber;
        }
        
    
    public void Sum(TreeNode root, long sum){
        if(root == null) return;
        sum -= root.val;
        if(sum == 0){
            pathnumber++;           
        }
        Sum(root.left,sum);
        Sum(root.right,sum);
    } 
}

方法二：深度优先搜索
访问每一个节点 node，检测node为起始节点且向下延深的路径有多少种，递归遍历每一个节点的所有可能的路径，然后将这些路径数目加起来即为返回结果。

1. 定义 rootSum(p,val)表示以节点 p为起点向下且满足路径总和为 val的路径数目，对二叉树上每个节点 p 求出 rootSum(p,targetSum)，然后对这些路径数目求和即为返回结果。
2. 对节点 p 求rootSum(p,targetSum)时，以当前节点 p 为目标路径起点，不断递归向下进行搜索。假设当前的节点 p 的值为 val，对左子树和右子树进行递归搜索，对节点 p 的左孩子节点 p_left求出 rootSum(p_left,targetSum−val)，以及对右孩子节点 p_right求出 rootSum(p_right,targetSum−val)。节点p 的 rootSum(p,targetSum)即等于rootSum(p_left,targetSum−val)与rootSum(p_right,targetSum−val)之和，同时还需要判断一下当前节点 p 的值是否刚好等于 targetSum
3. 采用递归遍历二叉树的每个节点 p，对节点 p 求 rootSum(p,val)，然后将每个节点所有求的值进行相加求和返回。

java代码如下：

class Solution {
	//同理参数类型也是用long,否则有一个变态的测试用例通不过
    public int pathSum(TreeNode root, long targetSum) {//pathSum表示最终的结果，包含每一个节点的结果
        if (root == null) {
            return 0;
        }

        int res = rootSum(root, targetSum);
        res += pathSum(root.left, targetSum);
        res += pathSum(root.right, targetSum);
        return res;
    }

    public int rootSum(TreeNode root, long targetSum) {//rootSum表示当前节点开始往下的路径数目
        int res = 0;

        if (root == null) {
            return 0;
        }
        int val = root.val;
        if (val == targetSum) {
            res++;
        }

        res += rootSum(root.left, targetSum - val);
        res += rootSum(root.right, targetSum - val);
        return res;
    }
}

方法三：前缀和（牛牛牛）

对方法二中的重复计算进行优化

前缀和，就是到达当前元素的路径上，之前所有元素的和

在同一个路径之下，如果两个数的前缀总和是相同的，那么这些节点之间的元素总和为零，进一步推广， 如果前缀总和为currSum，在节点A和节点B处相差target，则位于节点A和节点B之间的元素之和是target。

抵达当前节点(即B节点)后，将前缀和累加，然后查找在前缀和上，有没有前缀和currSum-target的节点(即A节点)，存在即表示从A到B有一条路径之和满足条件的情况。结果加上满足前缀和currSum-target的节点的数量，然后递归进入左右子树

java代码如下：

class Solution {
    public int pathSum(TreeNode root, int targetSum) {
    	// key是前缀和, value是大小为key的前缀和出现的次数
        Map<Long, Integer> prefix = new HashMap<Long, Integer>();
        prefix.put(0L, 1);//前缀和为0的一条路径,即当targetSum 等于某个节点值时，curPrefix - targetSum = 0,即当前节点前缀和为0，但是当前节点自己也算做一条符合条件的路径，所以也要计数
        return dfs(root, prefix, 0, targetSum);
    }

    public int dfs(TreeNode root, Map<Long, Integer> prefix, long curr, int targetSum) {
        //递归终止的条件
        if (root == null) {
            return 0;
        }
        int res = 0;
        curr += root.val;//当前节点的前缀和

        res += prefix.getOrDefault(curr - targetSum, 0);//currSum-target相当于找路径的起点，只搞到了满足的起点，则当前点到起点的距离就是target，即存在一条满足题意的路径，res++
        prefix.put(curr, prefix.getOrDefault(curr, 0) + 1);// 更新路径上当前节点前缀和的个数
        
        //进入下一层
        res += dfs(root.left, prefix, curr, targetSum);
        res += dfs(root.right, prefix, curr, targetSum);

        prefix.put(curr, prefix.getOrDefault(curr, 0) - 1);//回到本层，恢复状态，去除当前节点的前缀和数量
        return res;
    }
}