论文阅读：《Evaluation of a momentum based impact model and application in an effectivity study》-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_39378221/article/details/128756413

论文提出了一种基于动量守恒和恢复系数的冲击模型，用于判断交通事故的严重性，特别适用于ADAS系统的有效性研究。通过与PC-Crash软件的对比验证，模型显示出了较高的精度。未来的研究方向包括三维模型扩展、参数敏感性研究及碰撞点定义的优化。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

论文名字太长了，标题打不下了。。。

《Evaluation of a momentum based impact model and application in an effectivity study considering junction accidents 》

1 背景

这篇论文是以ADAS（Advanced Driver Assistance Systems）作为背景展开的，驾驶辅助系统，直观上看应该算是L3级别。

作为辅助驾驶系统，有各种各样的问题需要解决，比如说“什么样的事故可以避免，什么样的避免不了”。这种。而“仿真”可以提供大量不同的场景去帮助测试。而这篇文章主要讨论的问题就是，如何去判断一个事故的严重性。

本文明确提出其目标：提出一个基于动量守恒方程和恢复原理的冲击模型，并探讨其在ADAS有效性研究中的适用性。

2 方法

2.1 一些基本规则

本文使用的方法类似于我之前学习的车辆事故分析和重建方法。也是一套基于动量守恒的建模方式。个人理解这篇文章就属于该理论的一种应用。对于这套冲击模型，做出以下假设：

该模型只考虑两车之间交换的接触力
轮胎力忽略不计
碰撞持续时间被假设为无限小
不计算形变
模型只考虑二维

1）动量&角动量守恒

无外力系统动量和角动量应该是守恒的：

$\vec p = \vec p_1 + \vec p_2 + \cdots + \vec p_n\\ \vec L = \vec L_1 + \vec L_2 + \cdots + \vec L_n$

2）恢复系数

碰撞分为两个阶段，压缩阶段和恢复阶段。压缩阶段产生形变，直到接触面相对速度为0。接下来就是恢复阶段。那这里的恢复系数 $e$ 被定义为两个阶段动量变化量的比值：
$\frac{\vec S_{rest}}{\vec S_{komp}}$

这个恢复系数看起来和车辆事故分析和重建方法中的形式不同，前者是动量变化量的比值，后者是碰撞前后两车相对速度的比值。这里先记录下来，后续有机会深入探索一下恢复系数。

2.2 基于动量的冲击模型

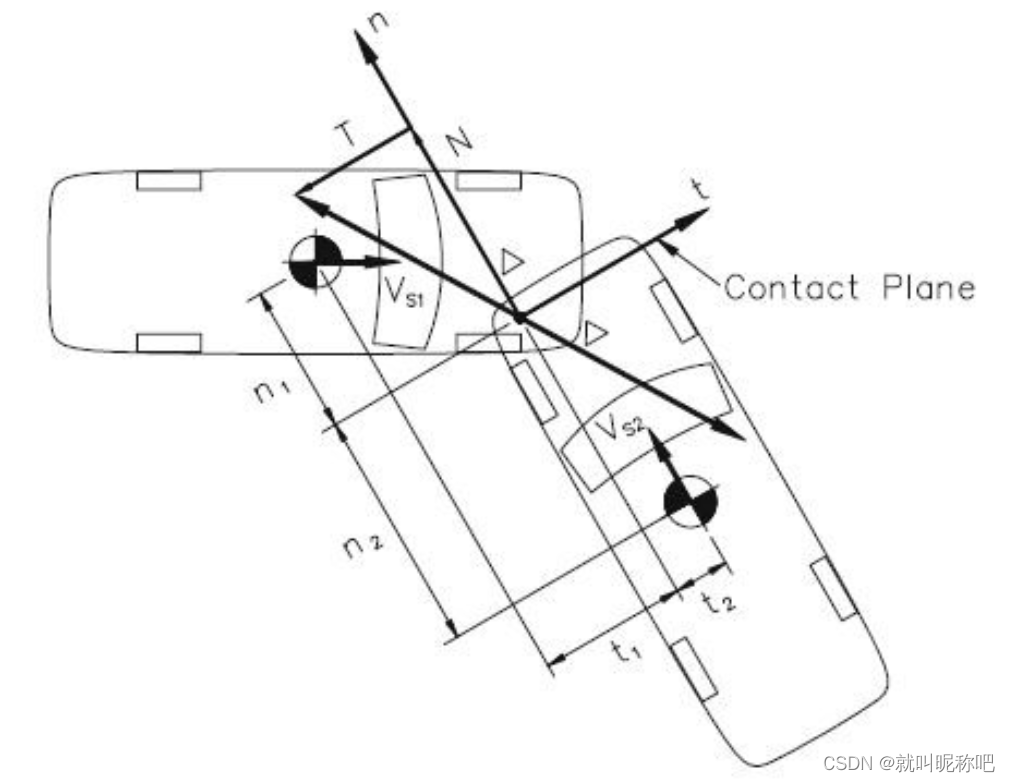
类似地，n-t坐标系与车辆事故分析和重建方法中看样子是一致的，如下图。t是接触面切线方向，n是接触面法向方向。两车重心 $(center\ of\ gravity,\ cog)$ 速度在n和t方向速度分量可以通过点积求得，其中 $\phi$ 代表速度在原始坐标系下的角度：

$v_{Tcog1} = v_{cog1}\cdot \begin{pmatrix}cos(\phi_1)\\sin(\phi_1)\end{pmatrix} \cdot \vec t \\ v_{Ncog1} = v_{cog1}\cdot \begin{pmatrix}-sin(\phi_1)\\cos(\phi_1)\end{pmatrix} \cdot \vec n$

然后在接触点的那个位置的速度，算上角速度可以求得：

$v_{T1} = v_{Tcog1} + w_1n_1\\ v_{N1} = v_{Tcog1} - w_1t_1$

然后设 $I_1, I_2$ 是两个车的转动惯量，接下来文章列的守恒方程，和车辆事故分析和重建方法应该是一模一样的，字母用的不一样，不知道为什么不保持一致。这里不重复写了。

最后文章讨论了一下Full impact和Sliding collision。这里大概就是对应了车辆事故分析和重建方法中的impulse ratio这个概念。

2.3 定义接触点

因为这个方法应用的时候得选择n-t坐标系，那确定这个坐标原点就比较重要了。车辆事故分析和重建方法中这个点叫做Point C。本文叫POI，point of impact。这里是用的几何方法定义这个点。

请添加图片描述

我概括一下这个方法就是：

两车polygon重合点的质心作为POI
两车polygon的交点作直线CP（Contact Plane）代表t方向所在直线，有了t就有了n

这里多边形的质心求法文章是参考的维基百科给的方法，大概就是把多边形分割为三角形，然后将所有三角形重心坐标根据面积加权这个方法。（不过我看这个式子的下标范围怎么怪怪的，一共
$n$ 个点，那式子里竟然会出现 $x_n$ ）

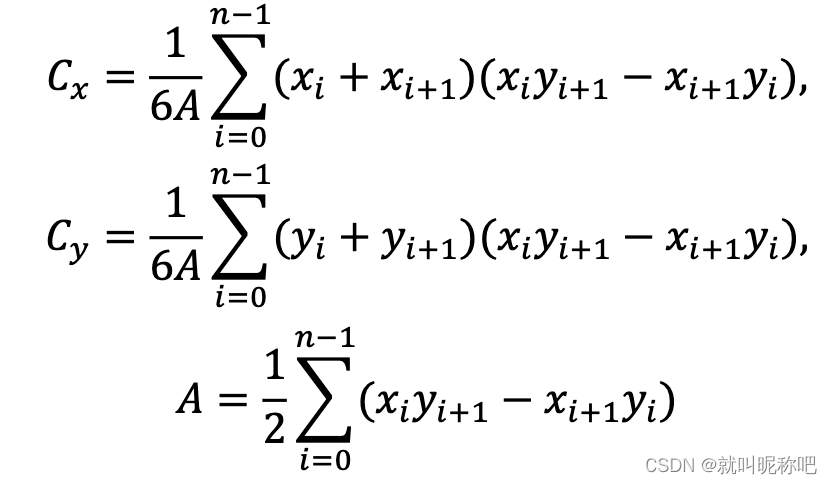
另外，文章使用仿真方法去做这件事情，那这个重合的位置是怎么选的呢？文章里提到After initial contact, the simulation is continued without impact calculation for a certain amount of time (also called penetration depth)。也就是说，在刚刚接触时刻，再往后运行一小段时间叫做penetration depth，选择这个位置作为求解位置。

3 方法验证

本文用了一个叫做PC-Crash的软件去验证这个建模方法算得到底好不好。这个PC-Crash作为一个事故重建软件，在业界内是广泛被接受的。然后这个事故数据是从CEDATU (Central Database for In-Depth Accident Study)这里拿的，这里的事故应该都被PC-Crash重建过了的。

本文一共选择36个事故，去评估这个建模方法，算出来的结果发现，本文的方法和PC-Crash算出来的，在小数点后几个点位是相同的。（这么准的吗？）

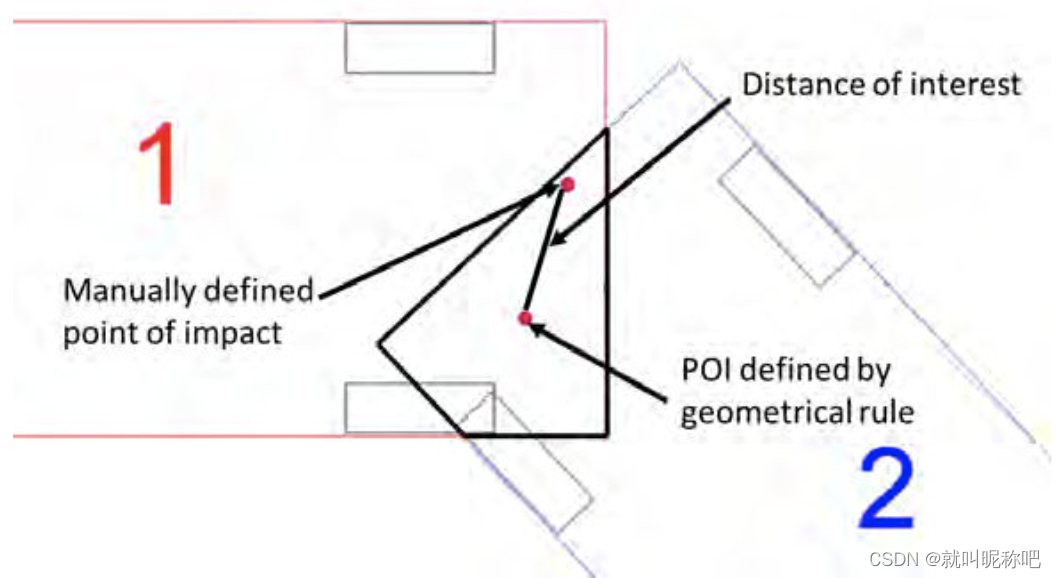
本文还探究了这个POI和CP对计算结果的灵敏度。大概就是这样子，用人选的点和几何规则选择的点去对比。然后看这个Distance of interest和 $\Delta v$ 的变化关系，如下图所示。

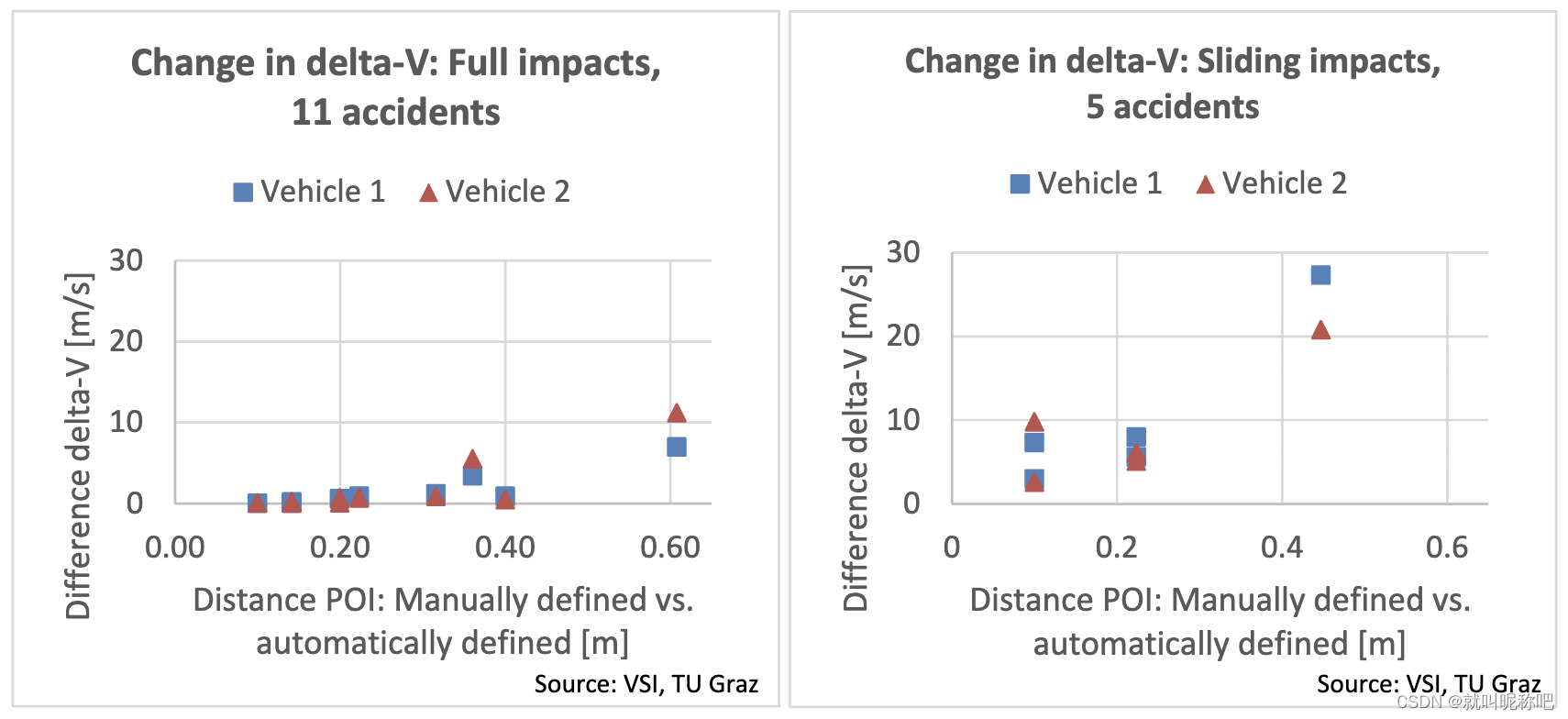
看下对比结果吧。这里把Full impact和Sliding impact分开来看了。看得出来，这个Sliding impact的计算结果对POI更敏感，因为distance变大了之后，这个 $\Delta v$ 变了能有25m/s。对于Full impact，这个distance的变化浮动在21里面到26里面之间看样子都是可接受的。

请添加图片描述