剑指Offer51—数组中的逆序对

剑指offer51

题意

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

解题思路

很容易想到，双层for循环暴力统计，但是此方法时间复杂度为O(N^2)，题目给定的数组长度范围 0≤N≤50000 ，可知此复杂度是不能接受的。

「归并排序」与「逆序对」是息息相关的。归并排序体现了 “分而治之” 的算法思想，具体为：

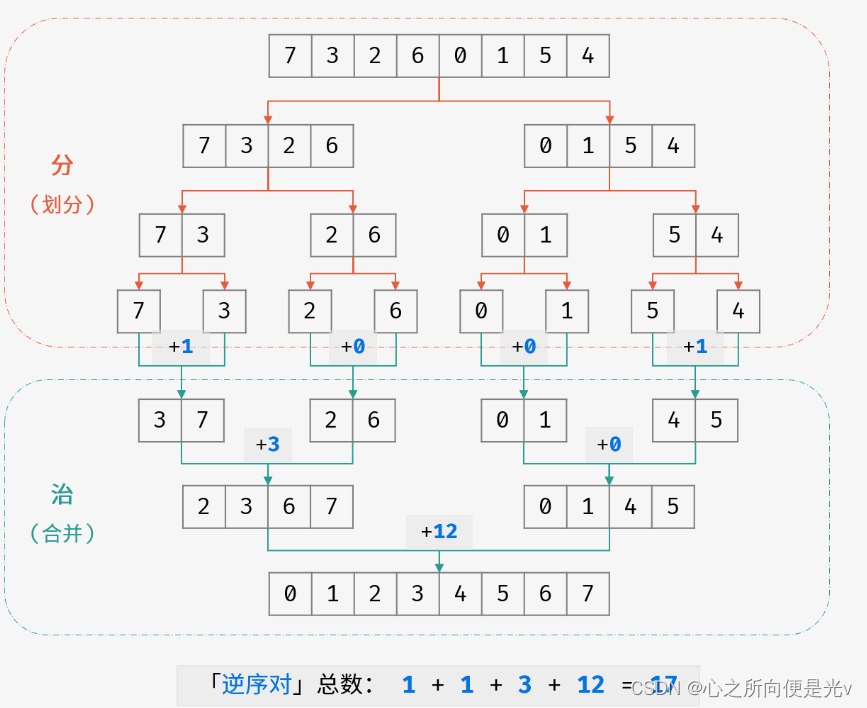
• 分： 不断将数组从中点位置划分开（即二分法），将整个数组的排序问题转化为子数组的排序问题；
• 治： 划分到子数组长度为 1 时，开始向上合并，不断将 较短排序数组 合并为 较长排序数组，直至合并至原数组时完成排序；

例如：

合并阶段 本质上是 合并两个排序数组 的过程，而每当遇到 左子数组当前元素 > 右子数组当前元素 时，意味着 「左子数组当前元素 至 末尾元素」 与 「右子数组当前元素」 构成了若干 「逆序对」 。（因为合并阶段，左右子数组都是有序的，所以上述所说成立）。

因此，考虑在归并排序的合并阶段统计「逆序对」数量，完成归并排序时，也随之完成所有逆序对的统计。

---

算法流程： 

merge_sort() 归并排序与逆序对统计：

1. 终止条件： 当 l≥r 时，代表子数组长度为 1 ，此时终止划分；
2. 递归划分： 计算数组中点 m ，递归划分左子数组 merge_sort(l, m) 和右子数组 merge_sort(m + 1,r);
3. 合并与逆序对统计：
   1. 暂存数组 nums 闭区间 [l, r] 内的元素至辅助数组 tmp ；
   2. 循环合并： 设置双指针 i , j 分别指向左 / 右子数组的首元素；
      1. 当 i = m + 1 时： 代表左子数组已合并完，因此添加右子数组当前元素 tmp[j] ，并执行 j = j + 1 ；

      2. 否则，当 j = r + 1 时： 代表右子数组已合并完，因此添加左子数组当前元素 tmp[i] ，并执行 i = i + 1 ；

      3. 否则，当 tmp[i]≤tmp[j] 时： 添加左子数组当前元素 tmp[i]，并执行 i = i + 1；

      4. 否则（即 tmp[i] > tmp[j]）时： 添加右子数组当前元素 tmp[j] ，并执行 j = j + 1 ；此时构成 【m - i + 1】个「逆序对」，统计添加至 res；

4. 返回值： 返回直至目前的逆序对总数 res；

---

reversePairs() 主函数：

1. 初始化： 辅助数组 tmp ，用于合并阶段暂存元素；
2. 返回值： 执行归并排序 merge_sort() ，并返回逆序对总数即可；

---

复杂度分析： 

• 时间复杂度 O(NlogN) ： 其中 N 为数组长度；归并排序使用 O(NlogN) 时间；
• 空间复杂度 O(N) ： 辅助数组 tmp 占用 O(N) 大小的额外空间；

C++实现

class Solution 
{
public:
    int reversePairs(vector<int>& nums) 
    {
        vector<int> tmp(nums.size());   //初始化tmp，用于在合并阶段暂存排序之前的元素
        return merge_sort(0,nums.size()-1,nums,tmp);    
    }
    int merge_sort(int l,int r,vector<int>& nums,vector<int>& tmp)
    {
        //递归出口，如果只有一个元素了，直接返回0（即0个逆序对）
        if(l>=r)
            return 0;

        //1、划分阶段

        //计算数组中点m，然后递归划分左右子数组
        int m = l+(r-l)/2;
        //开始递归划分左右子数组，直到左右子数组只有一个元素就开始合并
        int res = merge_sort(l,m,nums,tmp)+merge_sort(m+1,r,nums,tmp);

        //2、合并阶段

        //首先暂存 [l,r] 区间的元素，这是未归并之前的元素，这段区间包含了左右子数组的所有元素
        for(int index=l;index<=r;++index)
            tmp[index]=nums[index];
        //然后开始循环合并，设置 i,j 指针分别指向左、右子数组的起始位置，然后依次比较各自所指元素大小
        int i = l;  //左子数组起始位置
        int j = m+1;    //右子数组起始位置s=
        //开始合并数组（即更新nums的[l,r]区间，使之变得有序），并且统计逆序对总数
        for(int k=l;k<=r;++k)
        {
            //如果左子数组合并完毕，即 i=m+1，则添加右子数组当前元素 tmp[j]到nums[k]，添加后，j的位置要加一
            if(i==m+1)
                nums[k]=tmp[j++];
            else if(j==r+1) //右子数组合并完毕，添加左子数组当前元素到nums[k]
            {
                nums[k]=tmp[i++];
            }
            else if(tmp[i]<=tmp[j]) //左子数组要小一些，就将小一点的元素添加到 nums[k]
            {
                nums[k]=tmp[i++];
            }
            else if(tmp[i]>tmp[j])  
            //右子数组的当前元素小，就讲右子数组当前元素添加到nums[k]，并且左子数组当前元素到m位置的所有元素都比右子数组的
            //当前元素大（因为左右子数组是有序的），所以共有 (m-i+1)个逆序对。
            {
                nums[k]=tmp[j++];
                res+=m-i+1;
            }
        }
        //跳出for循环后，代表nums数组的 [l,r] 区间已经归并完毕，该区间的元素是有序的。此时返回逆序对即可
        return res;
    }
};