链表和数组基础

链表

链表是数据结构之一，其中的数据呈线性排列。在链表中，数据的添加和删除都较为方便，就是访问比较耗费时间。

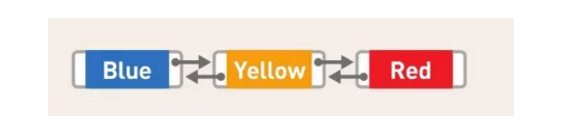
如上图所示就是链表的概念图，Blue、Yellow、Red 这 3 个字符串作为数据被存储于链表中，也就是数据域，每个数据都有 1 个指针，即指针域，它指向下一个数据的内存地址，其中 Red 是最后 1 个数据，Red 的指针不指向任何位置，也就是为 NULL，指向 NULL 的指针通常被称为空指针。

在链表中，数据一般都是分散存储于内存中的，无须存储在连续空间内。

因为数据都是分散存储的，所以如果想要访问数据，只能从第 1 个数据开始，顺着指针的指向一一往下访问（这便是顺序访问）。比如，想要找到 Red 这一数据，就得从 Blue 开始访问，这之后，还要经过 Yellow，我们才能找到 Red。

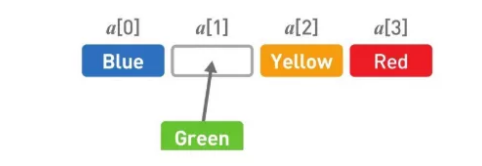
如果想要添加数据，只需要改变添加位置前后的指针指向就可以，非常简单。比如，在 Blue 和 Yellow 之间添加 Green。

首先将 Blue 的指针指向的位置变成 Green，然后再把 Green 的指针指向 Yellow，数据的添加就大功告成了。

数据的删除也一样，只要改变指针的指向就可以，比如删除 Yellow。

这时，只需要把 Green 指针指向的位置从 Yellow 变成 Red，删除就完成了。虽然 Yellow 本身还存储在内存中，但是不管从哪里都无法访问这个数据，所以也就没有特意去删除它的必要了。今后需要用到 Yellow 所在的存储空间时，只要用新数据覆盖掉就可以了。

那么对链表的操作所需的运行时间到底是多少呢？在这里，我们把链表中的数据量记成 n。访问数据时，我们需要从链表头部开始查找（线性查找），如果目标数据在链表最后的话，需要的时间就是 O（n）。

另外，添加数据只需要更改两个指针的指向，所以耗费的时间与 n 无关。如果已经到达了添加数据的位置，那么添加操作只需花费 O（1）的时间，删除数据同样也只需 O（1）的时间。
链表扩展

以上讲述的链表是最基本的一种链表，除此之外，还存在几种扩展方便的链表。

虽然上文中提到的链表在尾部没有指针，但我们也可以在链表尾部使用指针，并且让它指向链表头部的数据，将链表变成环形，这便是循环链表，也叫环形链表。循环链表没有头和尾的概念，想要保存数量固定的最新数据时通常会使用这种链表。

循环链表
另外，以上提到的链表里的每个数据都只有一个指针，但我们可以把指针设定为两个，并且让它们分别指向前后数据，这就是双向链表。使用这种链表，不仅可以从前往后，还可以从后往前遍历数据，十分方便。

但是，双向链表存在两个缺点：一是指针数的增加会导致存储空间需求增加；二是添加和删除数据时需要改变更多指针的指向。

双向链表
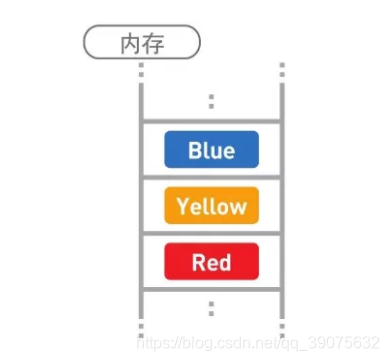
数组

如上就是数组的概念图，Blue、Yellow、Red 作为数据存储在数组中，其中 a 是数组的名字，后面 [] 中的数字表示该数据是数组中的第几个数据，该数字也就是数组下标，下标从 0 开始计数，比如 Red 就是数组 a 的第 2 个数据。

那么为什么许多编程语言中的数组都从 0 开始编号的呢？先别急，可以先自己思考下，将会在文末进行讲解。

从图中可以看出来，数组的数据是按顺序存储在内存的连续空间内的。

由于数据是存储在连续空间内的，所以每个数据的内存地址（在内存上的位置）都可以通过数组下标算出，我们也就可以借此直接访问目标数据，也就是随机访问。

比如现在我们想要访问 Red，如果是链表的话，只能使用指针就只能从头开始查找，但在数组中，只需要指定 a[2]，便能直接访问 Red。

但是，如果想在任意位置上添加或者删除数据，数组的操作就要比链表复杂多了。这里我们尝试将 Green 添加到第 2 个位置上。

首先，在数组的末尾确保需要增加的存储空间。

为了给新数据 Green 腾出位置，要把已有数据一个个移开，首先把 Red 往后移。

然后把 Yellow 往后移。

最后在空出来的位置上写入 Green。

添加数据的操作就完成了。

反过来，如果想要删除 Green 呢？

首先，删掉目标数据 Green。

然后把后面的数据一个个往空位移，先把 Yellow 往前移。

接下来移动 Red。

最后再删掉多余的空间，这样一来 Green 便被删掉了。

补充

这里讲解一下对数组操作所花费的运行时间，假设数组中有 n 个数据，由于访问数据时使用的是随机访问（通过下标可计算出内存地址），所以需要的运行时间仅为恒定的 O（1）。

通过数组下标计算出内存地址的寻址公式如下：

a[i]_address = base_address + i * data_type_size

其中 base_address 为内存块的首地址，data_type_size 表示数组中每个元素的大小。

但另一方面，想要向数组中添加新数据时，必须把目标位置后面的数据一个个移开。所以，如果在数组头部添加数据，就需要 O（n） 的时间，删除操作同理。

在链表和数组中，数据都是线性地排成一列。在链表中访问数据较为复杂，添加和删除数据较为简单；而在数组中访问数据比较简单，添加和删除数据却比较复杂。

我们可以根据哪种操作较为频繁来决定使用哪种数据结构。

最后，让我们一起来思考下刚开始提到的问题：为什么很多编程语言中数组都从 0 开始编号？

解惑

从数组存储的内存模型上来看，“下标”最确切的定义应该是“偏移（offset）”。如果用 a 来表示数组的首地址，a[0] 就是偏移为 0 的位置，也就是首地址，a[k] 就表示偏移 k 个 type_size 的位置，所以计算 a[k] 的内存地址只需要用这个公式：

a[k]_address = base_address + k * type_size

但是，如果数组从 1 开始计数，那我们计算数组元素 a[k] 的内存地址就会变为：

a[k]_address = base_address + (k-1)*type_size

对比两个公式，可以发现，从 1 开始编号，每次随机访问数组元素都多了一次减法运算，对于 CPU 来说，就是多了一次减法指令。

数组作为非常基础的数据结构，通过下标随机访问数组元素又是其非常基础的编程操作，效率的优化就要尽可能做到极致。所以为了减少一次减法操作，数组选择了从 0 开始编号，而不是从 1 开始。

除此之外还有历史原因，C 语言设计者用 0 开始计数数组下标，之后的 Java、JavaScript 等高级语言都效仿了 C 语言，或者说，为了在一定程度上减少 C 语言程序员学习 Java 的学习成本，因此继续沿用了从 0 开始计数的习惯。实际上，很多语言中数组也并不是从 0 开始计数的，比如 Matlab。甚至还有一些语言支持负数下标，比如 Python。