[小样本图像分割]Few-Shot Semantic Segmentation with Prototype Learning

Few-Shot Semantic Segmentation with Prototype Learning（BMVC2018）

本文是后面很多小样本图像分割的框架的基础，也就是使用原型进行匹配的思想。

论文地址

摘要

语义分割为每个图像像素分配一个类标签。这种密集的预测问题需要大量的手动注释数据，而这些数据往往不可用。Few-Shot学习的目的是学习一个只有几个带标签样本的新类别。在本文中，我们将Few-Shot语义分割问题从one-way(一类)发展到n-way(n类)。受Few-Shot分类的启发，我们提出了一种广义的Few-Shot语义分割框架和替代训练方案。该框架基于原型学习和度量学习。该方法在PASCAL VOC 2012数据集的one-sway Few-Shot语义分割中表现出了不错的性能。

存在的问题及解决方案

在Few-Shot分类中，每张图像只有一个标签。然而，在Few-Shot语义分割中，每幅图像可以包含多个语义类。在N-way K-shot语义分割任务中，有一个支持集和一个查询集。给定一个支持集，我们想要预测一个查询图像的N个类的分割掩码。以往关于Few-Shot语义分割的研究是N = 1的特例。

受之前关于Few-Shot分类的工作启发，我们有两个问题:1)我们可以用度量学习方法来解决这个问题吗2)我们能否将Few-Shot语义分割从1-way扩展到N-way?

在[以往文献中中，加权最近邻分类器（weighted nearest neighbor classifiers）是基于投影函数(通常是CNN)学习到的度量来构建的。因此，由于像素级最近邻分类的计算成本高，推理阶段的速度慢，不能直接将Few-Shot分类器应用到Few-Shot分割中。对于第二个问题，由于人类可以通过有限的观察分辨出多达30000种物体类别之间的区别，所以对于机器而言，通过模仿人类视觉特性，从1-way扩展到N-way是有可能的。

我们采用双分支架构。第一个分支是原型学习器，它将图像和注释作为输入并输出原型。第二个分支是分割网络，它以新图像和原型作为输入并输出分割掩码。

由于支持集包含在训练阶段未见过的类，过拟合是影响性能的瓶颈。在我们的模型中，原型学习器既扮演语义信息的特征提取器的角色，也扮演防止过拟合的正则器的角色。通过使用距离度量学习和非参数最近邻分类，我们在不增加参数数量的情况下进一步提高了性能。我们还提出了一种用于n-way任务的数据增强技术称为排列训练（permutation training）

问题定义

假定$S={\left\{\left(x^i,y^i\right)\right\}}_{i=1}^{N_s}$表示支持集，其中$x^i$表示一张$[H^i,W^i,3]$的图像，$y^i$表示$x^i$对应的标注。$y^i$是一张$[H^i,W^i,1]$大小的对应特定语义类的二值掩码。$x^q$是一张$[H^i,W^i,3]$大小的不包含在S中的查询图像。由于$x^i$可能包含多个语义类而标注$y^i$指对应一个类，我们允许$x^i=x^j$只要$y^i\ne y^j$。我们选择这种设计是为了简化和泛化，因为包含多个类的注释可以分解为多个单类注释。

Few-Shot语义分割问题可以推广为N-way K-shot学习任务。每种方法为N个类(不包括背景)中的每一个类提供K个图像掩码对，这些类在训练中不出现。也就是说支持集最终包含$N_s=N\times k$张图像。给定一张新图像，目的是为了学习一个分割模型$\mathcal{F}$来预测对于N个类的分割掩码。这个目标可以解释为学习一个$S\backsim \mathcal{F}\left(\cdot ,S\right)$映射。给定一个$x^q$，这个映射将定义一个输出的概率分布$\mathcal{F}\left(x^q,S\right)$。这里，不同于S中的单类注释的二进制掩码，$\mathcal{F}\left(x^q,S\right)$和作为ground-truth$的y^q$有相同的形状$[H^q,W^q,N+1]$。

对于训练过程中的每个episode，首先随机选择N个类。然后基于这N个被选择的类来随机选择一个支持集$S$和一张查询图像及其标注对$(x^q,y^q)$。因此训练目标是最小化像素级的多类交叉损失$J$:

其中$j$遍历空间位置（坐标）， c ∈ { 1 , . . . , N + 1 } c\in \left\{ 1,...,N+1 \right\} c∈{1,...,N+1}。

在一般的监督学习和半监督学习设置下，训练数据和测试数据具有相同的类。在一个标准的FCN中， ∀ c ∈ { 1 , . . . , N + 1 } \forall c\in \left\{ 1,...,N+1 \right\} ∀c∈{1,...,N+1}，$c$只映射到一个类别(包括背景)。由特征提取器产生的特征映射被投影到一个(N +1)通道空间。分割模型学习从图像中的原始像素到投影空间对应的空间位置的映射。在分类顺序固定的情况下，膨胀卷积、多尺度融合和级联体系等技术可以在监督学习环境下掌握更多的语义特征，特别是在训练数据量较大的情况下。然而，在Few-Shot的学习任务中，测试数据具有在训练中未见过的类，这些监督技术很容易导致过拟合。我们在Few-Shot的语义分割中存在一个看似矛盾的问题。我们想要建立一个语义分割模型，但我们不希望模型记住所有在训练过程中学习到的语义信息。

方法

我们提出了一种基于原型学习的N-way K-shot语义分割框架。在认知科学中，原型是指一个范畴中比其他范畴更具有代表性的一些元素。这里，原型是一个具有高阶判别信息的特征向量。在有限的监督下，我们以一种方式训练网络，对语义类的预测也就是接近这一语义类在特定投影空间上的原型。 整体网络架构如下图所示：

这是一个2-way 1-shot任务，（a）是原型学习分支，原型学习分支对给定支持集的查询集进行分类，并学习原型。（b）是一个分割分支，利用查询图像和从(a)中学习的原型来输出预测分割掩码。（c）演示了权重$W$如何用于计算概率图的融合。每个概率图都与查询图像相连接，然后输入原型学习器以产生一个特征向量，相似度量函数$d$取特征向量和原型来输出相似度评分。

基础架构

假定$f_{\theta }$表示一个含有参数$\theta$的特征提取器，$f_{\theta }$将输入映射到一个含$M$个通道的特征图。然后使用全局平均池化（GAP）来从特征图中过滤出空间信息，其输出为一个$M$维的特征向量。假定$S_c$是$S$的一个只包含语义类$c$的子集，我们定义类$c$的原型作为该类的均值特征向量:

其中$|S_c|=k$，$g_{\varphi }$表示分割分支中参数为$\varphi$的另一个特征提取器。理论上$f_{\theta }$和$g_{\varphi }$有不同的结构，如果输出通道数量相同的化。我们使用上采样层来将原型恢复到和特征图$g_{\varphi }\left(x^q\right)$相同大小。然后通过element-wise addition将$g_{\varphi }\left(x^q\right)$和N个恢复的原型相融合。特别地，为了将背景(BG)与原型区分开，我们从$g_{\varphi }\left(x^q\right)$中减去所有原型的均值特征向量。假设$m$代表语义类(包括背景)的特征映射，我们有：

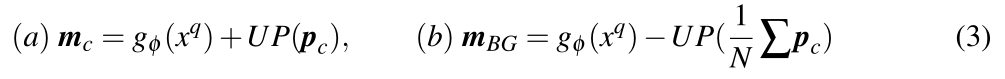
$m$被1×1卷积层(conv)压缩成单通道特征图。连接的N +1通道特征映射在每个通道中具有不同的重要程度，因此对每个通道进行L2范数归一化。我们建议使用1×1卷积和双线性插值来产生最终对数。通过使用1×1卷积，我们可以利用高效的GPU实现，并融合不同通道之间的信息。让$l_{\alpha }$表示对数的第$\alpha$的通道，softmax和nβ表示归一化后的特征图的β通道，我们有：

度量学习

原型被定义在投影空间，通过$f_{\theta }$的距离度量来学习。我们可以通过在原型学习分支中学习一个更好的距离度量来学习更多有代表性的原型。除了N个语义类的原型，我们还引入了一个原型作为背景。S中的原始图像和代表背景的二进制掩码形成一个新的集合$S_{BG}=\left\{\left(x^i,y_{BG}^i\right)\right\}$。BG的原型同样是用公式（2）计算的，其中$|S_{BG}|=Nk$，在得到原型$p$后，我们使用非参数加权最近邻分类器对语义类进行分类。对于N-way学习任务，$y^q$能被分解成N+1个二值掩码$y_c^q$，其中 c ∈ { 1 , . . . , N + 1 } c\in \left\{ 1,...,N+1 \right\} c∈{1,...,N+1}。优化的目标是最大化：

其中$d$表示相似度量函数，设$J_{\theta }^{cls}$为原型学习者分支的辅助损耗，并与来自分割分支的$J_{\varphi }^{seg}(x^q,y^q)$进行交替优化:

其中$I_{c=t}$是一个二值指示函数。

由于BG类有自己的原型，我们使用公式3重新定义$m_{BG}$，我们观察到双线性插值之前的最后1×1 conv可以被解释为像素加权最近邻分类。与其学习$W$，我们提出使用一种非参数技术，类似于原型学习分支中使用的方法，以减少过拟合。我们用元素的sigmoid操作替换了单通道特征映射上的L2归一化并固定θ：

并且${\hat{y}}_{\beta }^q$表示对于类$\beta$的预测概率分布。很容易发现${\sum }_{\beta }^{}{W}_{\beta ,\alpha }=1$,$W$是有界约束的也就是说它并不需要参数调整。在给定原型和$f_{\theta }$时，概率图用于计算它们自身融合的$W$。从这个意义上说，这种架构也可以看作是一种自我注意机制。与基础模型相比，没有额外的参数，但原型可以掌握更多的判别特征，分割分支将逐步将其特征空间移向原型的特征空间。

排列训练（Permutation Training）

在监督学习任务中，采用了数据增强技术来避免过拟合。这些技术通常对原始图像进行修改，如对原始图像添加噪声、进行几何变换以及使用部分图像。在此，我们提出了置换训练在Few-Shot语义分割中的应用。对于一个N-way的学习任务，其中有N+1个类。在训练中，单通道特征映射的连接有一个顺序(哪个类先来，哪个类最后来)，这取决于原型的输入顺序。也就是说一共有$(N+1)!$种排列方式。对于一个episode，有$S$和$(x^q,y^q)$，我们使用不同的原型顺序来训练模型。在实践中，当N很大时，我们随机选择整个排泄的子集。这种技术背后的核心思想是使网络能够区分不同的原型，而不是记忆所有的语义信息。整个训练流程的概述见算法1。原型学习分支是为了产生原型的判别性表示给分割分支。