BFS、DFS学习及Python实现

广度优先遍历（BFS）

  顾名思义，BFS总是先访问同一层的结点，然后向外扩展访问下一层结点，它最有用的性质是可以遍历一次就生成中心结点到所遍历结点的最短路径，这一点在求无权图的最短路径时非常有用。

from queue import Queue

def bfs(graph, start):
    # 创建一个set记录点是否已被遍历
    visited = set()
    q = Queue()
    q.put(start)
    while not q.empty():
        u = q.get()
        print(u)
        for v in graph.get(u, []):
            if v not in visited:
                visited.add(v)
                q.put(v)

graph = {1: [4, 2], 2: [3, 4], 3: [4], 4: [5]}
bfs(graph, 1)

算法步骤：

1. 创建一个队列，选择遍历的起点插入到队列中。
2. 创建一个记录节点是否被遍历过的set，以防止节点被多次遍历形成（多次遍历亦有可能陷入死循环）。
3. 当队列不为空时，从队中弹出节点并输出以记录。并依次遍历将该节点的下一层节点，依次插入到队尾。插到队尾之前需要先检查该子节点是否已被遍历，遍历过则不插入，没遍历过则插入并在visited集合中记录该点。
4. 重复3直到队列为空，此时所有节点均被遍历，并且是“由内向外”。

复杂度分析：

需要注意的是复杂度的好坏取决于图的存储结构，也就是图是以邻接表存储还是以邻接矩阵存储。（还有其他的存储结构，这里只讨论比较常见的这两种）

遍历图的过程实质上是对每个顶点查找其邻接点的过程，其耗费的时间取决于所采用结构

---

下面节选自：https://www.cnblogs.com/zhuozengsi/p/4619616.html

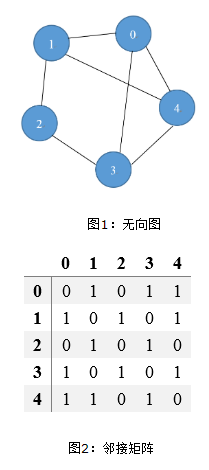
邻接矩阵：顾名思义，是一个矩阵，一个存储着边的信息的矩阵，而顶点则用矩阵的下标表示。对于一个邻接矩阵M，如果M(i,j)=1，则说明顶点i和顶点j之间存在一条边，对于无向图来说，M (j ,i) = M (i, j)，所以其邻接矩阵是一个对称矩阵；对于有向图来说，则未必是一个对称矩阵。邻接矩阵的对角线元素都为0。

邻接表：

1. 邻接表就是为图中的每个顶点关联一个链表，其中记录这个顶点的所有邻边。
2. 在无向图中，同一条边被邻接表存储两次。在有向图中，同一条边被邻接表存储一次。
3. 在无向图中，顶点的度即为：对应链表中结点的个数。在有向图中，顶点出度即为：对应链表中结点的个数；入度则需要遍历其他顶点的链表。

  对于顶点数很多但是边数很少的图来说，用邻接矩阵显得略为“奢侈”，因为矩阵元素为1的很少，即其中的有用信息很少，但却占了很大的空间。所以下面我们来看看邻接表，以上图的无向图为例，邻接表如下：

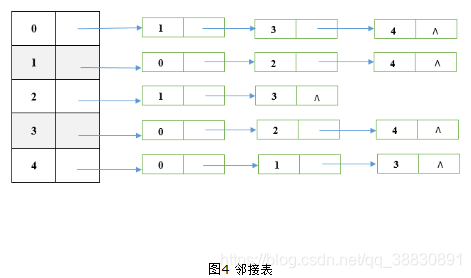
可以看出:

1. 邻接矩阵的优点：便于计算出各个顶点的度，以及判断两个顶点间是否有边
   邻接矩阵的缺点：图的边如果很少时，矩阵会存在大量0（只是为了说明边不存在），从而造成大量的空间浪费
2. 邻接表的优点：只存储实际的边，节省空间（有多少存多少）。
   邻接表的缺点：确定顶点的度时，需要遍历整个链表（对于有向图，确定入度时，需要遍历其他节点的链表，很复杂）。
3. 稠密用邻接矩阵，稀疏用邻接表

---

继续回到复杂度的讨论

• 时间复杂度：

1. 邻接表存储时，从一个顶点开始搜索时，访问未被访问过的节点，最坏情况下是所有邻接点均未被访问过（即遍历所有点所有边后才找到终点），这时每个邻接点和边均要被访问一次（邻接表是一维数组存节点，链表存边（节点间关系）来实现的），所以T=O（V+E），其中V是顶点数，E是边数。
2. 邻接矩阵存储时，查找每个顶点的邻接点所需时间为O(V)（邻接矩阵是由二维数组存储边，一维数组存储点来实现的），即遍历该节点所在的该行该列。又有n个顶点，故算总的时间复杂度为O(|V|^2)。

• 空间复杂度：
  无论是在邻接表还是邻接矩阵中存储，都需要借助一个辅助队列，V个顶点均需入队，最坏的情况下，空间复杂度为O（V）。

深度优先遍历（DFS）

  深度优先遍历算法dfs通俗的说就是“顺着起点往下走，直到无路可走就退回去找下一条路径，直到走完所有的结点”。这里的“往下走”主是优先遍历结点的子结点。bfs与dfs都可以完成图的遍历。dfs常用到爬虫中。

def dfs(graph, start):
	# 创建一个set记录点是否已被遍历
    visited = set()
    # python没有直接实现栈，这里使用list模拟栈操作
    # 入栈就是向列表中append一个元素，出栈就是pop列表中最后一个元素
    stack = [[start, 0]]
    print(start)
    while stack:
        v, next_idx = stack[-1]
        # 临界条件：图中点没有下一个邻接点或者邻接点全部遍历完毕
        if (v not in graph) or (next_idx >=len(graph[v])):
            stack.pop()
            continue
        next = graph[v][next_idx]
        # 记录当前节点的邻接点入栈数量
        stack[-1][1] += 1
        if next in visited:
            continue
        print(next)
        visited.add(next)
        stack.append([next, 0])

graph = {1: [4, 2], 2: [3, 4], 3: [4], 4: [5]}
dfs(graph, 1)

算法步骤：

1. 创建一个记录遍历节点的set，与BFS同理。再创建一个数组，此数组是为了模仿栈的操作。数组中包含一个个的含有两个元素的子数组，子数组中第一个元素存图的节点，第二个元素存图节点的邻接点遍历情况（0表示邻接点还未遍历，1表示已经有1个邻接点被遍历，以此类推，此元素作为临界判断的条件）。
2. 若栈不为空，且节点在图中拥有邻接点，则将邻接点记录到栈中（append），并标记此邻接点已被遍历；每次记录一个邻接点时，对节点的遍历数字+1；若遍历到底了，也就是当前节点没有邻接点了，则开始从栈中弹出元素（pop）。
3. 弹出到开始节点时，一条“深路径”就被遍历出来了。继续从开始节点的下一个邻接点继续向“深处”遍历。需要注意的是，从开始节点的2号邻接点遍历时，需要记录开始节点已经遍历两个邻接点了！
4. 重复第3步，当开始节点没有邻接点可以遍历时，将开始节点弹出，此时栈为空，深度优先遍历结束。

复杂度分析：

• 时间复杂度：

1. 邻接表表示时，查找所有顶点的邻接点所需时间为O(E)，访问顶点的邻接点所花时间为O（V）,此时，总的时间复杂度为O(V+E)。
2. 邻接矩阵表示时，查找每个顶点的邻接点所需时间为O(V)，要查找整个矩阵，故总的时间复杂度度为O(V^2)

• 空间复杂度：
  DFS算法时一个递归算法，需要借助递归工作栈，所以它的空间复杂度为O(V)