第2章.选择排序
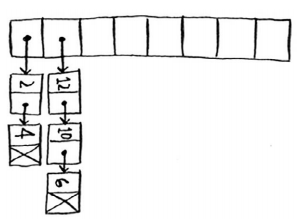
- 链表与数组混合型的数据结构适合存储用户信息。此数据结构在查找时比数组慢,比链表快;在插入数据时,比数组快,与链表差不多(仅多一步查找字母所在数组位置)
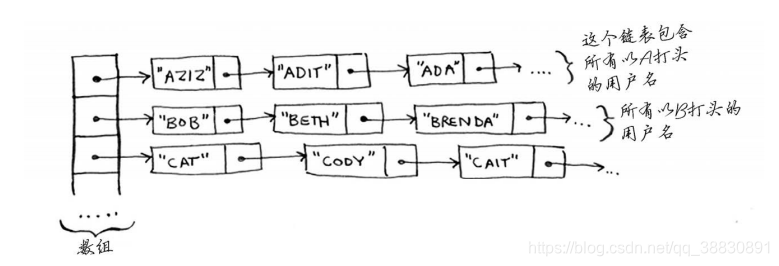
该数据结构并非静态链表,静态链表如下:
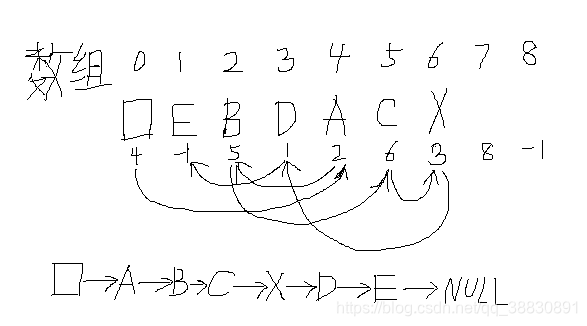
- 选择排序时间复杂度为O(n^2)
def findSmallest(arr):
# 存储最小的值
smallest = arr[0]
# 存储最小元素的索引
smallest_index = 0
for i in range(1, len(arr)):
if arr[i] < smallest:
smallest = arr[i]
smallest_index = i
return smallest_index
def selectionSort(arr):
"""
选择排序
:param arr:
:return:
"""
newArr = []
for i in range(len(arr)):
# 找到数组中最小的元素,并将其加到新数组中
smallest = findSmallest(arr)
# arr.pop()用以删除数组元素并获取其对应值
newArr.append(arr.pop(smallest))
return newArr
print(selectionSort([5, 3, 6, 2, 10]))
第3章.递归
- 为了防止递归程序陷入死循环,必须告诉它何时停止递归。因此每个递归函数都有两部分:基线条件和递归条件
基线条件:函数不再调用自己
递归条件:函数调用自己
例:
def countdown(i):
print(i)
if i <= 0: # 基线条件
return None
else: # 递归条件
countdown(i-1)
- 调用栈
def greet2(name):
print("how are you, ", name, "?")
def bye():
print("ok bye!")
def greet(name):
print("hello, ", name, "!")
greet2(name)
print("getting ready to say bye...")
bye()
greet("test")
调用过程如下:
1.假设调用greet(“test”),计算机将为该函数分配一块内存;
2.在该内存中,变量name被设置成test,并写进内存中;
3.接下来顺序执行greet函数,打印“hello,test!”,再调用greet2(name),此时的;name=test。计算机同样也会为greet2分配一块内存;
4.计算机使用一个 栈来表示函数的内存分配。其中greet2在栈顶,greet在栈底。执行greet2,打印“how are you,test?”,然后从函数调用返回,栈顶(greet2)内存块弹出;
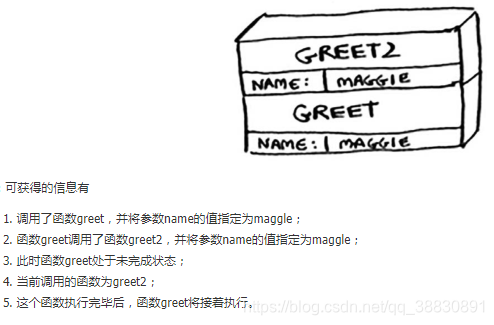
5.现在栈顶的内存块是函数greet,这意味着刚才greet2执行完之后返回到了greet中。因此,当调用greet2时,函数greet只执行了一部分。所以需要记住一个重要的概念:调用另一个函数时,当前函数暂停并处于未完成状态;
6.该函数的所有变量值都还在内存中(name=“test”),执行完函数greet2时,返回函数greet中,并从离开的地方继续执行程序,打印“getting ready to say bye…”,进而继续调用bye()函数;
7.与调用greet2过程同理,计算机会为bye()函数分配新的内存,并置于函数调用栈顶,bye执行:打印“ok bye!”之后,从栈中弹出,继续执行greet的剩余部分。
8.由于greet剩余部分没有语句,故直接从greet函数返回(从调用栈中弹出)。此时调用栈为空,程序执行完毕。
- 练习题:
- 递归调用栈
def fact(x):
if x == 1:
return 1
else:
return x * fact(x-1)
print(fact(3))
执行过程:
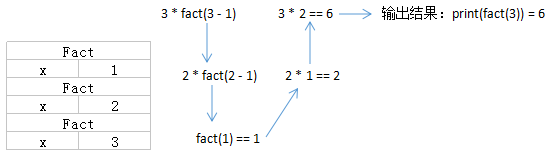
5.思考题:递归函数如果没有基线条件,则会无休止运行下去,会给栈带来什么影响?
答:会导致栈不断扩大(一直push新的函数调用)。由于每个程序使用的调用栈空间有限,程序用完这些空间后,将因栈溢出而终止
6.小结:
- 使用栈很方便,但是调用栈可能很长,所以使用递归时,往往会非常耗内存。想要优化性能有两种选择:
- 重写代码,改为循环
- 使用尾递归(高级递归)
第4章.快速排序
1. 分治法(D&C,divide and conquer)
插入Python知识点:
- == 与is的区别
- ==是python标准操作符中的比较操作符,用来比较判断两个对象的value(值)是否相等;is也被叫做同一性运算符,这个运算符比较判断的是对象间的唯一身份标识,也就是id是否相同。
- 只有数值型和字符串型的情况下,a is b才为True,当a和b是tuple,list,dict或set型时,a is b为False。
也就是说对于数值和字符串变量,is和==是可以互换的(因为变量值相等的同时id也相同);而对于tuple,list,dict或set,即使值相同,id也是不同的,这时is和==的效果就不一样了
-
列表的表示
a = [0,1,2,3,4,5,6,7,8,9]
b=a[i:j]表示a列表中i到j-1位置的元素,生成新的列表复制给b。如b=a[1:3]表示[1,2]。
- 当i缺省时,默认为0,即 a[:3]相当于 a[0:3]
- 当j缺省时,默认为len(alist), 即a[1:]相当于a[1:10]
- 当i,j都缺省时,a[:]就相当于完整复制一份a了b = a[i:j:s]这种格式,i,j与上面的一样,但s表示步进,缺省为1
所以a[i:j:1]相当于a[i:j]
当s<0时,i缺省时,默认为-1. j缺省时,默认为-len(a)-1
所以a[::-1]相当于 a[-1:-len(a)-1:-1],也就是从最后一个元素到第一个元素复制一遍。
- 使用分治法解决问题步骤:
(1).找出基线条件,对于数组的递归条件,一般基线条件是数组为空或者数组只包含一个元素。
(2).不断将问题分解,直到符合基线标准
- 例子:土地均分问题
假设你是农场主,你有如下1680m640m的农田,你需要将它划分成正方形的小方块,且保证每个方块面积相同。
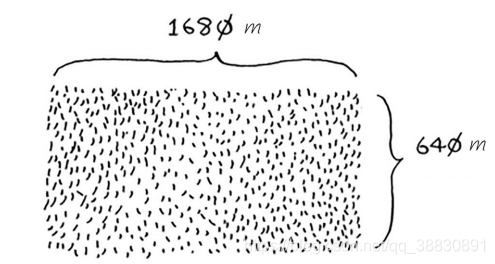
解决这种问题,首先找到基线标准,即一条边是另一条边的整数倍,此时恰好平分成正方形农田,如下图:
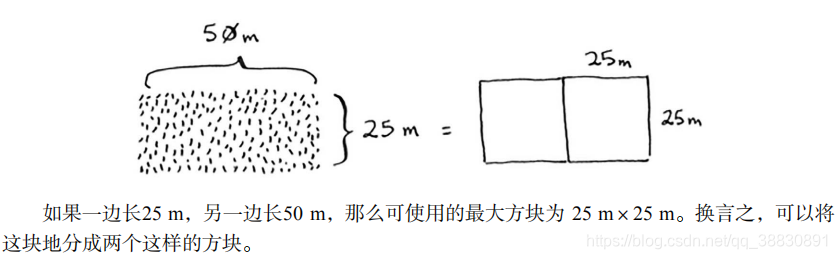
找到基准条件后,再找出递归条件,这是D&C的用武之地,即缩小问题规模。我们先找到这块地可容纳的最大方块,如下图:
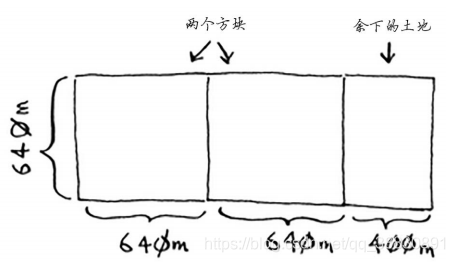
你可以从这块地中划出两个640 m×640 m的方块,同时余下一小块地。现在是顿悟时刻:何不对余下的那一小块地使用相同的算法呢?
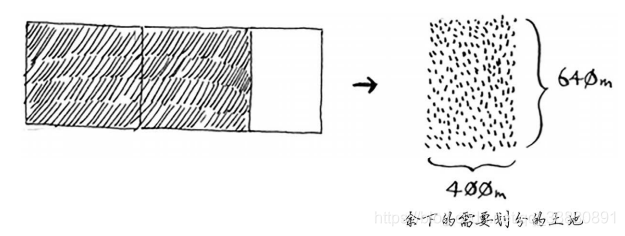
在经过多次划分后,最终划分的剩余土地可到基线条件,如下图:
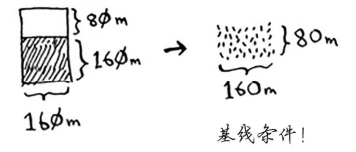
这块160m80m的土地就满足了基线条件,因为160是80的整数倍,对其进行划分的时候,正好可以划分出两个面积相等的80m80m的正方形土地,如下图:
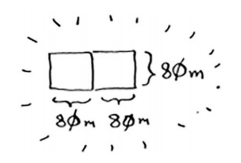
因此,对于最初的土地,适用的最大的方块为80m80m:
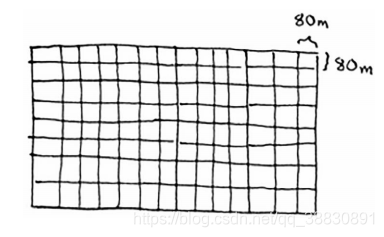
- 二分查找也是一种分而治之的思想。试找出二分查找算法的基线条件和递归条件
- 使用分治法解决问题步骤:
def binary_search(list, item, low, high):
"""
折半查找
:param list:查找的有序列表
:param item:查找元素
:param low:低
:param high:高
:return:
"""
# 基准条件
if low > high:
return None
else:
mid = (low + high) // 2
# 递归条件
if item > list[mid]:
return binary_search(list,item,mid+1,high)
elif item < list[mid]:
return binary_search(list,item,low,mid-1)
else:
return mid+1
2. 快速排序
def quicksort(array):
if len(array) < 2: # 基线条件:为空或只含有2个元素以下则有序
return array
else:
pivot = array[0] # 递归条件
less = [i for i in array[1:] if i <= pivot]
greater = [i for i in array[1:] if i > pivot]
return quicksort(less) + [pivot] + quicksort(greater)
print(quicksort([10,5,2,3,8,6]))
每次都选择列表中首个元素作为递归条件,并找到比该元素小的数组和比该元素大的数组,小的放在左边,大的放在右边,重新排列,再递归的再局部进行排序。
课后题:根据数组包含的元素创建一个乘法表,即如果数组为[2, 3, 7, 8, 10],首先将另一个数组中每个元素都乘以2,再将每个元素都乘以3,然后将每个元素都乘以7,以此类推
def multipation(arr, ele):
if len(arr) == 0:
return ele
for i in range(0,len(ele)):
ele[i] = ele[i] * arr[0]
arr.pop(0)
return multipation(arr, ele)
print(multipation([2,3,7,8,10], [1,1,1]))
运行结果:
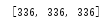
第5章.散列表
散列表是将数据以key,value的形式存到数组中(可以理解为json或python的字典),通过散列函数查找目标元素,以达到根据key查找任何value时间都为O(1)。散列函数不是我们理想意义上的y=f(x),他只是一个key到value的映射关系,其中的x和y可以是除了数字之外的其他数据类型。可以这么认为:散列表=散列函数+数组。
-
散列表的性能
散列表可能发生冲突,比如在一个长度为26的数组中,存储不同键对应的值(假设水果(按首字母存位置)对应的价格),水果完全可能出现首字母相同的情况,如下图:
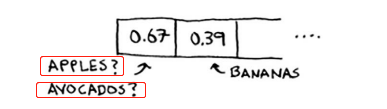
这种情况称为“冲突”,解决方法如下:
对冲突的位置建立链表
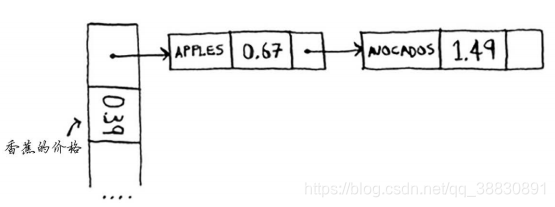
这种方式有缺陷,假设所有水果的首字母均相同,散列表就变成了一个很长的链表,此时查询速度会很慢。
导致上述情况的原因在于我们是按照水果首字母去决定水果存在数组中的位置的。这种映射关系是散列函数,正是因为选择了这种散列函数才会导致当所有首字母都相同时,散列表就变成了不适合做查询的链表。
这里的经验教训有两个:


所以综上所述,散列表的性能和散列函数有直接关系! -
良好的散列函数
散列表在最糟糕情况下和平均情况下的差别很大,下面是与数组、链表在查找、插入和删除操作上的时间复杂度:
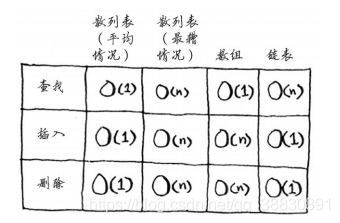
在平均情况下,散列表的查找(获取给定索引处的值)速度与数组一样快,而插入和删除速度与链表一样快,因此它兼具两者的优点!但在最糟情况下,散列表的各种操作的速度都很慢。因此,在使用散列表时,避开最糟情况至关重要。为此,需要避免冲突。而要避免冲突,需要有:
- 较低的填装因子
- 良好的散列函数
填装因子:
数组中元素数 / 数组长度
反应了数组利用率,一般填装因子大于0.7,就需要调整散列表的长度。散列函数:
良好的散列函数可以使数组呈均匀分布,糟糕的散列函数会使数组中的值“扎堆”,导致大量冲突。关于散列函数具体的实现好坏可自行深究。
第6章.广度优先搜索
解决最短路径问题的算法被称为广度优先搜索,它是一种用于图查找的算法。
-
广度优先搜索是"由近及远"的遍历思想。与起始位置直连的点先被遍历,所以其思想与队列完全吻合(先进先出)------【近的先检查,随即弹出】。
-
表示图节点使用散列表,键用来存储节点“名称”,而值用来存储边的权值(若为带权图)。
代码部分:
from collections import deque
def broad_first_search(name):
graph = { 'you':['alice','bob','claire'], 'bob':['anuj','peggy'],
'claire':['thom','jonny'], 'alice':['peggy'], 'anuj':[],
"peggy":[], "thom":[], "jonny":[] }
searched = []
search_queue = deque()
search_queue += graph[name]
while search_queue:
person = search_queue.popleft()
if not person in searched:
if person_is_seller(person):
print("%s is a mango seller"%(person))
return True
else:
search_queue += graph[person]
searched.append(person)
print("you haven't a mango seller friend")
return False
def person_is_seller(name):
return name[-1] == 'm'
broad_first_search('you')
运行时间:对整个图进行搜索,意味着每一条边都需要遍历到。另一方面,还需要使用一个队列,将所有的点添加到队列中去。这样整个时间复杂度为O(V+E),其中V为点的个数,E为边的个数。
第7章.迪杰斯特拉算法
广度优先搜索找出的是边数最少的路径。这是针对于非带权图。而对于带权图,往往我们要寻找权值最小的路径(也可以理解为最快路径),为此,可使用另一种算法—迪杰斯特拉算法。
注意:该算法只适用于不带负权边的有向无环图(directed acyclic graph,DAG)
对于带负权边的图,该算法无法找到最小路径(这里的小指代权值),这是因为迪杰斯特拉算法是建立在这样的假设之下:对于处理过的节点,不存在前往该节点的更小路径。但是这个假设只有在没有负权边时才成立!
迪杰斯特拉算法代码实现详解:
以下图为例用代码实现Dijkstra算法:
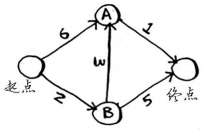
编写代码,需要借助3个散列表。分别存储整张图的结构、节点的开销、节点的父节点。
随着算法进行,将不断更新costs和parents表
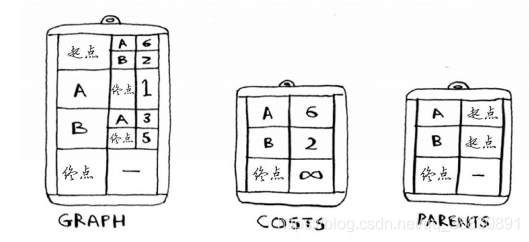
# 算法实现需要借助3个散列表
graph = {}
graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2
graph["a"] = {}
graph["a"]["end"] = 1
graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["end"] = 5
graph["end"] = {}
costs = {}
# float("inf")代表正无穷、float("-inf")或-float("inf")代表负无穷
infinity = float("inf")
costs["a"] = 6
costs["b"] = 2
costs["end"] = infinity
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["end"] = None
# 定义一个标记节点是否被遍历的列表
processed = []
def find_lowest_cost_node(costs):
lowest_cost_node = None
lowest_cost = float("inf")
for node in costs: # 遍历所有节点
cost = costs[node]
if cost < lowest_cost and node not in processed:
lowest_cost = cost
lowest_cost_node = node
return lowest_cost_node
def dijkstra():
# 在未处理的节点中找出开销最小的节点,其中costs为记录节点开销的列表(此步为初始化)
node = find_lowest_cost_node(costs)
# 在所有节点都被处理后结束
while node is not None:
# cost为节点当前开销
cost = costs[node]
# 找出当前节点的邻居
neighbors = graph[node]
for i in neighbors:
new_cost = cost + neighbors[i]
if new_cost < costs[i]:
# 如果对于邻居节点,有更小的开销,则更新
costs[i] = new_cost
# 同时将该邻居节点的父节点置为当前节点
parents[i] = node
# 遍历完所有邻居节点后标记该节点已被处理
processed.append(node)
# 继续查找下一个最小开销的节点
node = find_lowest_cost_node(costs)
# 所有节点均被遍历过后开销列表中终点对应的值为所求
return costs["end"]
cost = dijkstra()
print("从起点到终点的最短距离为%d"%(cost))
第8章.贪婪算法
贪婪算法的原理:每步都选择局部最优解,从而得到一个近似的全局最优解。这种算法适合有时候,你只需要找到一个能够大致解决问题的算法,此时贪婪算法正好可派上用场,因为它实现起来很容易,得到的结果又与正确结果相当接近。
1. 集合覆盖问题
假设你办了个广播节目,要让全美50个州的听众都收听得到。为此,你需要决定在哪些广播台播出。在每个广播台播出都需要支付费用,因此你力图在尽可能少的广播台播出。现有广播台名单如下:
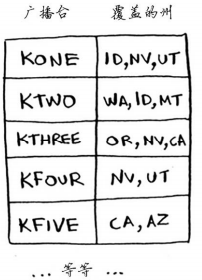
每个广播台都覆盖特定的区域,不同广播台的覆盖区域可能重叠。
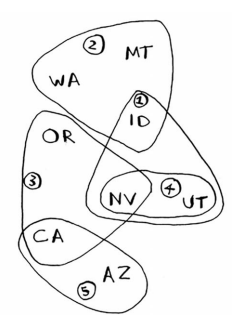
如何找出覆盖全美50个州的最小广播台集合呢?听起来很容易,但其实非常难。具体方法如下。
(1) 列出每个可能的广播台集合,这被称为幂集(power set)。可能的子集有2n
个。
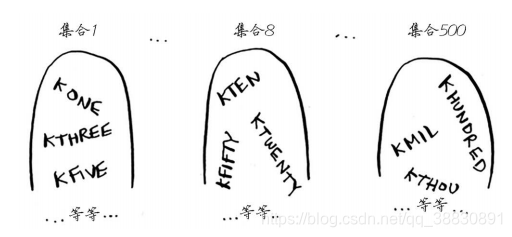
(2) 在这些集合中,选出覆盖全美50个州的最小集合。
问题是计算每个可能的广播台子集需要很长时间。由于可能的集合有2的n方个,因此运行时间为O(2^n)。如果广播台不多,只有5~10个,这是可行的。但如果广播台很多,结果将如何呢?随着广播台的增多,需要的时间将激增。假设你每秒可计算10个子集,所需的时间将如下。

上述问题没有任何一个算法可以足够快的去解决!而贪婪算法却可以用较短的时间得到一个近似解。
2. 利用贪婪算法解决问题
(1) 选出这样一个广播台,即它覆盖了最多的未覆盖州。即便这个广播台覆盖了一些已覆盖的州,也没有关系。
(2) 重复第一步,直到覆盖了所有的州。
这是一种近似算法(approximation algorithm)。在获得精确解需要的时间太长时,可使用近似算法。判断近似算法优劣的标准如下:
- 速度有多快
- 得到的近似解与最优解的近似程度
贪婪算法是不错的选择,它们不仅简单,而且通常运行速度很快。在这个例子中,贪婪算法的运行时间为O(n2),其中n为广播台数量。
代码实现:
# 州清单
states_needed = set(["mt", "wa", "or", "id", "nv", "ut", "ca", "az"])
# 广播台清单
stations = {}
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])
# 最终选择的广播台
final_stations = set([])
def greedy():
global states_needed
# 循环直到总集被全部涵盖
while states_needed:
# 每次遍历剩余广播台之前先将局部最优解清空
best_station = None
states_covered = set()
# 循环遍历广播台,选择局部最优解(每次都找包含州最多的那个台-在当前剩余总集中)
for station, states_for_station in stations.items():
covered = states_needed & states_for_station # coverd为交集
if len(covered) > len(states_covered):
best_station = station
states_covered = covered
# 将局部最优解添加到最终所求的Set中
final_stations.add(best_station)
# 将最优解已经包括的州从总集中删去
states_needed -= states_covered
greedy()
print(final_stations)
最终计算结果:

这个注意一下:集合类似于列表,只是不能包含重复的元素
3. NP完全问题(多项式复杂程度的非确定性问题)
为了解决集合覆盖问题,你必须计算每个可能的集合。这与旅行商问题很像:
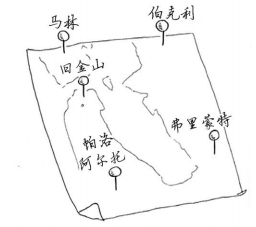
旅行商需要前往5个城市。他需要找出前往这5个城市的最短路径,为此,必须计算每条可能的路径长度。5个城市,可能的路径数是5的阶乘,也就是120个(注意,这个例子中起点和终点不确定,只要遍历完5个城市即可)。
这需要注意2个城市时:
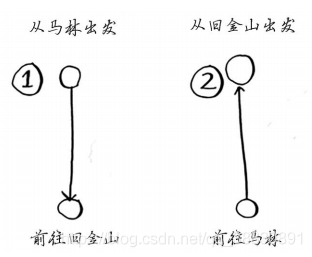
在旅行商问题中①和②是两条不同的路径。所以2个城市时可能的路线数为2!=2。
旅行商问题和集合覆盖问题有一些共同之处:你需要计算所有的解,并从中选出最小/最短的那个。这两个问题都属于NP完全问题。
在解决旅行商问题上,可以使用贪婪算法的思想:随便选择一个出发城市,然后每次选择要去的下一个城市时,都选择还没去的最近的城市。
NP完全问题的简单定义是:以难解著称的问题,如旅行商问题和集合覆盖问题。很多非常聪明的人都认为,根本不可能编写出可快速解决这些问题的算法。
4. NP完全问题的判定
对于最短路径问题(起点A,终点B),我们是可以使用迪杰斯特拉算法很容易求解出来的。但是如果把最短路径问题略微改动一下:需要求出经由指定几个点的最短路径,这就直接变成了旅行商问题了!----NP完全问题。所以,要明确判断是否为NP完全问题是没有办法的,但是可以通过一些经验来判断:
- 元素较少时算法的运行速度非常快,但随着元素数量的增加,速度会变得非常慢
- 涉及“所有组合”的问题通常是NP完全问题
- 不能将问题分成小问题,必须考虑各种可能的情况。这可能是NP完全问题
- 如果问题涉及序列(如旅行商问题中的城市序列)且难以解决,它可能就是NP完全问题
- 如果问题涉及集合(如广播台集合)且难以解决,它可能就是NP完全问题
- 如果问题可转换为集合覆盖问题或旅行商问题,那它肯定是NP完全问题
第9章.动态规划
1. 0-1背包问题
背包问题有两种:
- 第一种:假设有一个能装入容量为C的背包和n件重量分别为w1,w2,…,wn的物品,能否从n件物品中挑选若干件恰好装满背包,要求找出所有满足上述条件的解。
当C=10,各件物品重量为{1,8,4,3,5,2}时,可以找到下列4组解:(1,4,3,2)、(1,4,5)、(8,2)和(3,5,2)。
- 第二种:给定n种物品和一个背包。物品i的重量是wi,其价值为vi,背包的容量为C。应该如何选择装入背包中的物品,使得装入背包中物品的总价值最大?
上面的两个问题都是0-1背包问题,因为隐含的信息是:对每种物品只有两种选择,即装入背包或者不装入背包。不能将物品装入多次,也不能只装入部分的物品。
我们先来看第二种,找到价值最大的物品选择。这个问题可以用贪婪算法找到一个近似解,因为随着物品数目的增多,要想找到最优解,就需要将所有组合方案进行遍历,时间复杂度高达O(2^n)。但是对于这种问题,我们可以使用动态规划算法(DP)
2. 动态规划原理
动态规划的工作原理是先解决子问题,再逐步解决大问题。
























 3402
3402

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








