最小生成树( M i n i m u m Minimum Minimum S p a n n i n g Spanning Spanning T r e e Tree Tree,简称 M S T MST MST):构造连通网的最小代价生成树
找连通网的最小生成树,经典的有两种算法,普里姆算法和克鲁斯卡尔算法。
Prim算法
大致思想:设图 G G G顶点集合为 U U U,首先任意选择图 G G G中的一点作为起始点 a a a,将该点加入集合 V V V,再从集合 U − V U-V U−V中找到另一点 b b b使得点 b b b到 V V V中任意一点的权值最小,此时将 b b b点也加入集合 V V V;以此类推,现在的集合 V = a , b V={a,b} V=a,b,再从集合 U − V U-V U−V中找到另一点 c c c使得点 c c c到 V V V中任意一点的权值最小,此时将 c c c点加入集合 V V V,直至所有顶点全部被加入 V V V,此时就构建出了一颗 M S T MST MST。因为有 N N N个顶点,所以该 M S T MST MST就有 N − 1 N-1 N−1条边,每一次向集合 V V V中加入一个点,就意味着找到一条 M S T MST MST的边。
图解
下面以图解的形式来说明算法的思想:
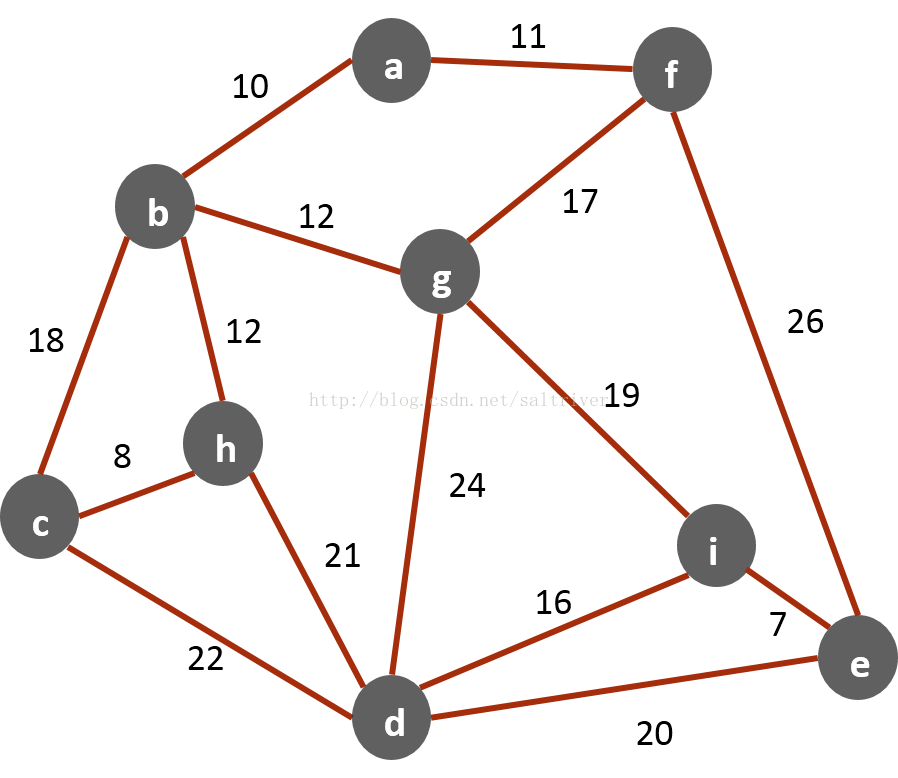
(1) 首先,顶点集合
U
U
U = {
a
,
b
,
c
,
d
,
e
,
f
,
g
,
h
,
i
a,b,c,d,e,f,g,h,i
a,b,c,d,e,f,g,h,i},然后选定一点(这里选择点
a
a
a)加入集合
V
V
V,即
V
V
V = {
a
a
a}, 寻找与
a
a
a相邻的所有边:
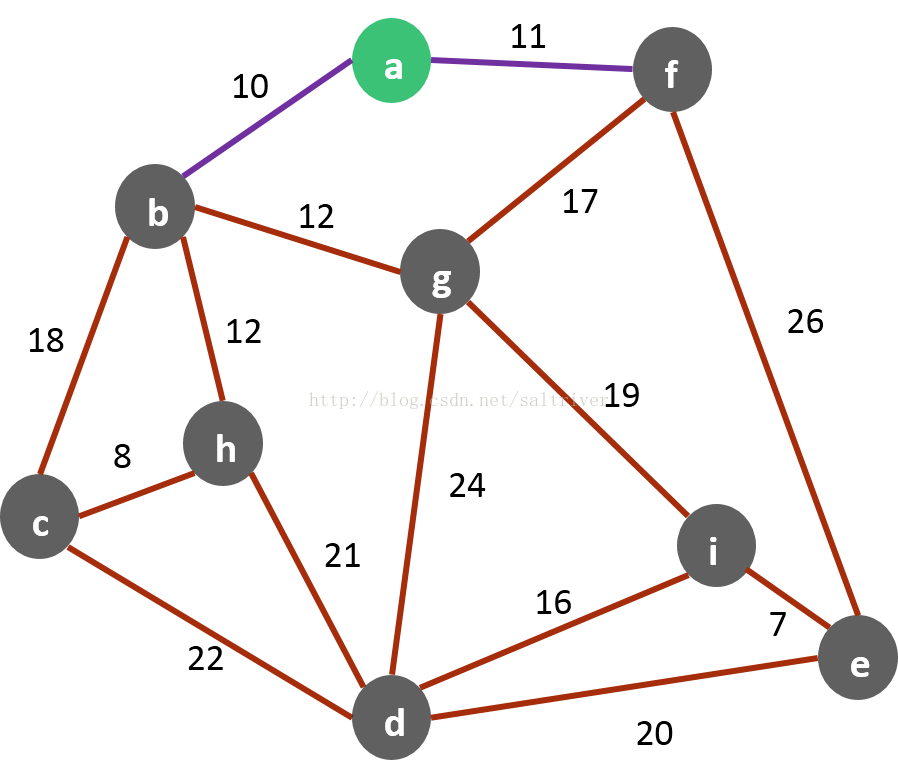
(2) 此时
V
V
V = {
a
a
a},
U
−
V
U - V
U−V = {
b
,
c
,
d
,
e
,
f
,
g
,
h
,
i
b,c,d,e,f,g,h,i
b,c,d,e,f,g,h,i},相邻的边有
a
−
b
a-b
a−b、
a
−
f
a-f
a−f,将
a
−
b
a-b
a−b加入最小生成树,同时将权值更小的边的顶点加入集合
V
V
V,此时
V
V
V = {
a
,
b
a,b
a,b}
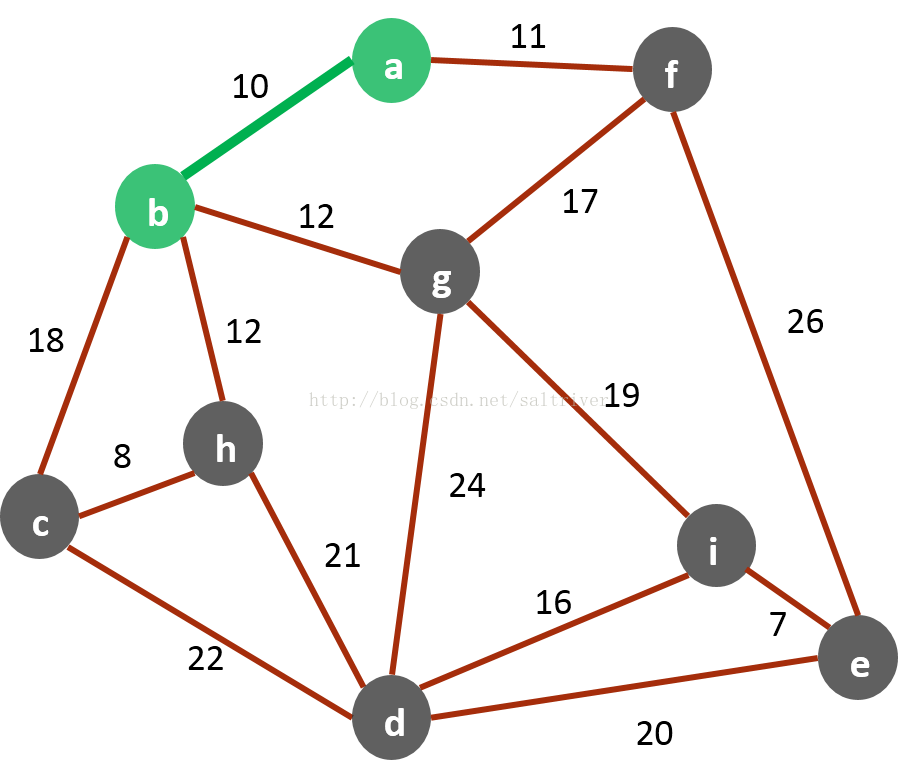
(3) 寻找
V
V
V中顶点与
U
−
V
U-V
U−V中顶点的所有边,如下图所示:
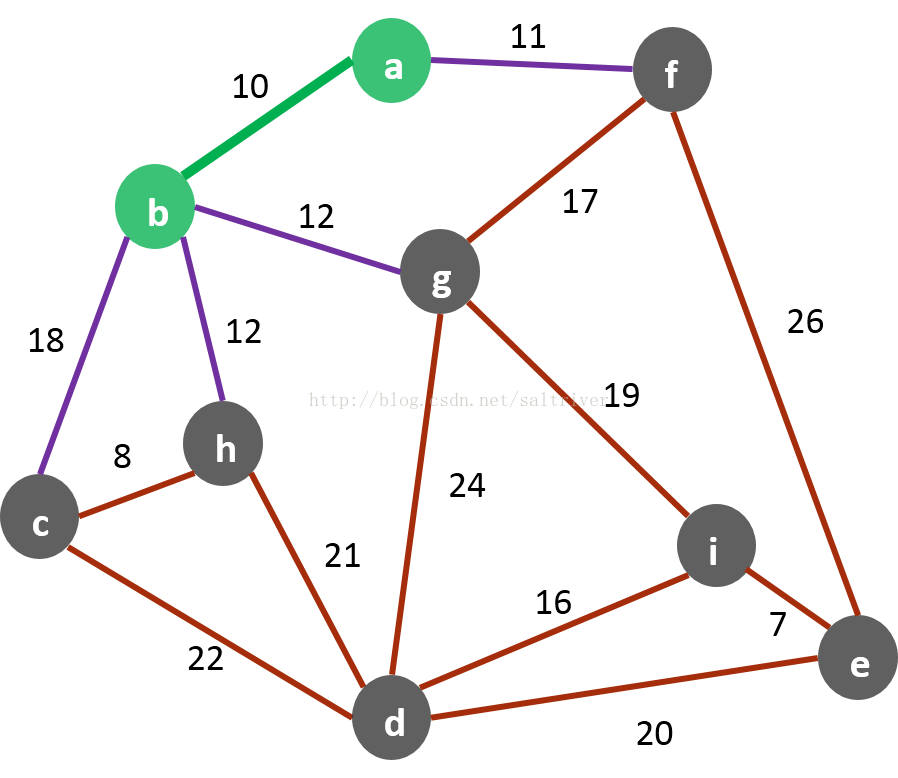
(4) 寻找权值最小的一条边的顶点加入
V
V
V,此时
V
V
V = {
a
,
b
,
f
a,b,f
a,b,f}
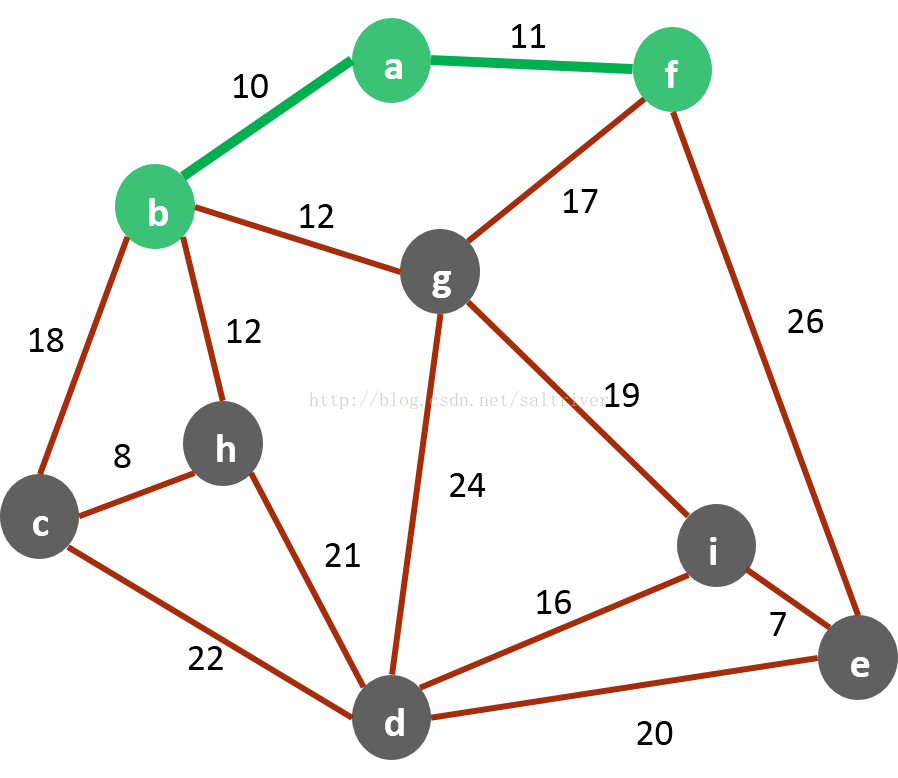
(6) 如此反复循环,直到
V
=
U
V=U
V=U,最终结果如下:
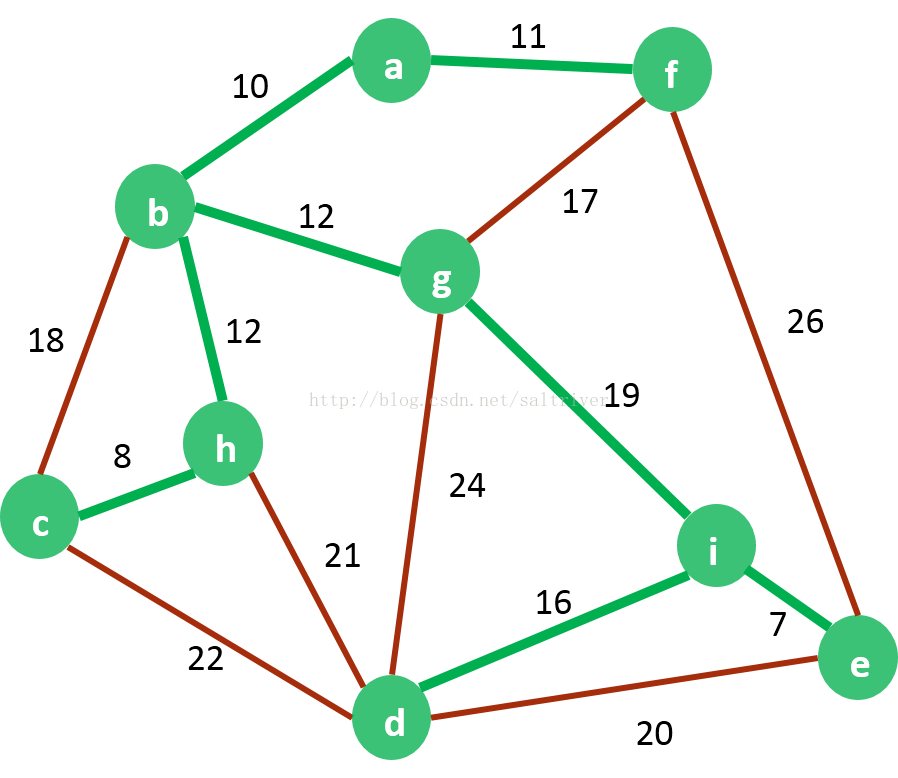
算法实现
在这里我们采用邻接矩阵的方式来实现
以上述图解示例做出如下结构:
#define MAXVEX 100 //最大顶点数
#define INFINITY 65535 //代替无穷
int graph[MAXVEX][MAXVEX]; //图
char map[] = { 'a', 'b', 'c', 'd', 'e', 'f', 'g',' h', 'i' }; //对应的顶点的描述
Prim算法的描述:
l o w c o s t [ i ] lowcost[i] lowcost[i]:表示以i为终点的边的最小权值,当 l o w c o s t [ i ] = 0 lowcost[i]=0 lowcost[i]=0说明以 i i i为终点的边的最小权值 = 0 =0 =0,也就是表示 i i i点加入了 M S T MST MST
a d j v e x [ i ] adjvex[i] adjvex[i]:表示对应 l o w c o s t [ i ] lowcost[i] lowcost[i]的起点,即说明边 < a d j v e x [ i ] , i > <adjvex[i],i> <adjvex[i],i>是 M S T MST MST的一条边,当 a d j v e x [ i ] = k adjvex[i]=k adjvex[i]=k表示起点 i i i加入 M S T MST MST, k k k表示权值小的顶点下标
int Prim(int graph[][MAXVEX], int n) {
int i, j, k, min, sum = 0;
int adjvex[MAXVEX];
int lowcost[MAXVEX];
//从下标为0的顶点开始,即从a开始
lowcost[0] = 0;
//初始化第一个顶点下标为0
adjvex[0] = 0;
//循环下标除0外的所有顶点
for (i = 1; i < n; ++i) {
//将v0顶点与之有边的权值存入数组
lowcost[i] = graph[0][i];
adjvex[i] = 0;
}
for (i = 1; i < n; ++i) {
min = INFINITY; //初始化最小权值为无穷
j = 1, k = 0;
//循环全部顶点,找到最小权值
while (j < n) {
if (lowcost[j] != 0 && lowcost[j] < min) {
min = lowcost[j];
k = j;
}
++j;
}
//输出最小权值边
cout << map[adjvex[k]] << "->" << map[k] << "=" << min << endl;
sum += min;
lowcost[k] = 0; //将下标为k的顶点加入MST
//更新lowcost为加入的顶点的所有边
for (j = 1; j < n; ++j) {
if (lowcost[j] != 0 && graph[k][j] < lowcost[j]) {
lowcost[j] = graph[k][j];
adjvex[j] = k;
}
}
}
return sum;
}
完整代码:
#include <iostream>
#include <fstream>
using namespace std;
#define MAXVEX 100
#define INFINITY 65535
int graph[MAXVEX][MAXVEX];
char map[] = { 'a', 'b', 'c', 'd', 'e', 'f', 'g',' h', 'i' };
int Prim(int graph[][MAXVEX], int n) {
int i, j, k, min, sum = 0;
int adjvex[MAXVEX];
int lowcost[MAXVEX];
lowcost[0] = 0;
adjvex[0] = 0;
for (i = 1; i < n; ++i) {
lowcost[i] = graph[0][i];
adjvex[i] = 0;
}
for (i = 1; i < n; ++i) {
min = INFINITY;
j = 1, k = 0;
while (j < n) {
if (lowcost[j] != 0 && lowcost[j] < min) {
min = lowcost[j];
k = j;
}
++j;
}
cout << map[adjvex[k]] << "->" << map[k] << "=" << min << endl;
sum += min;
lowcost[k] = 0;
for (j = 1; j < n; ++j) {
if (lowcost[j] != 0 && graph[k][j] < lowcost[j]) {
lowcost[j] = graph[k][j];
adjvex[j] = k;
}
}
}
return sum;
}
int main(int argc, char**argv) {
int i, j, k, cost;
int m, n;
ifstream in("input.txt");
in >> n >> m; //输入顶点个数及边的数量
//初始化邻接矩阵
for (i = 0; i < n; ++i) {
for (j = 0; j < n; ++j) {
graph[i][j] = INFINITY;
}
}
//构建图
for (k = 0; k < m; ++k) {
in >> i >> j >> cost;
graph[i][j] = cost;
graph[j][i] = cost;
}
cost = Prim(graph, n); //调用Prim算法
cout << "Minimum weight sum: " << cost << endl;
return 0;
}
i n p u t . t x t input.txt input.txt
9 15
0 1 10
0 5 11
1 2 18
1 6 12
1 7 12
2 3 22
2 7 8
3 4 20
3 6 24
3 7 21
3 8 16
4 5 26
4 8 7
5 6 17
6 8 19
o u t p u t output output
a->b=10
a->f=11
b->g=12
b-h=12
h->c=8
g->i=19
i->e=7
i->d=16
Minimun weight num: 95
由算法代码中的循环嵌套可以得知此算法的时间复杂度为 O ( n 2 ) O(n^2) O(n2)








 本文深入讲解了Prim算法,一种用于寻找最小生成树的经典算法。通过详细步骤和图解,阐述了如何从连通图中构建最小代价生成树。并提供了算法的实现代码,包括邻接矩阵的使用和时间复杂度分析。
本文深入讲解了Prim算法,一种用于寻找最小生成树的经典算法。通过详细步骤和图解,阐述了如何从连通图中构建最小代价生成树。并提供了算法的实现代码,包括邻接矩阵的使用和时间复杂度分析。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








