简单易懂排序算法（二）【简单选择排序】

简单选择排序：就是通过n-i次关键字间的比较，从n-i+1个记录中选出关键字最小的记录，并和第i（1<= i <= n）个记录交换

换而言之，即每次选出一个关键字最小的放在未排序的序列的首部

来看代码：

void SelectSort(vector<int>& vec)
{
	int n = vec.size();
	int minIndex;
	for (int i = 0; i < n - 1; ++i)
	{
		minIndex = i;
		for (int j = i + 1; j < vec.size(); ++j)
		{
			if (vec[j] < vec[minIndex])
				minIndex = j;
		}
		if (i != minIndex)
			swap(vec[i], vec[minIndex]);
	}
}

从代码简单分析：选用minIndex每次记录未排序的序列中最小关键字的下标，然后将其放在这一段未排序序列的首部与之前的序列构成一个有序序列

一个简单的测试：
测试序列：9，1，5，8，3，7，4，6，2

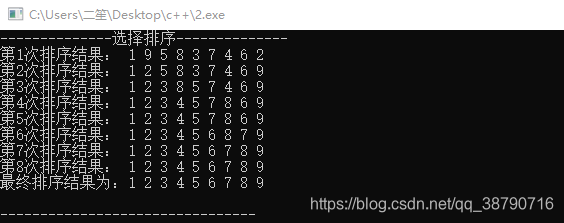
时间复杂度分析

从简单选择排序的过程来看，它最大的特点就是交换移动数据次数相当少，这样也就节约了许多时间。

分析它的时间复杂度：

• 无论最好亦或最差情况，其比较次数都是一样的多，第i趟排序需要进行$n-i$次的比较，此时需要比较：

$\sum _{i=1}^n(n-i)$ = n-1 + n-2 +… + 1 = $\frac{n(n-1)}{2}$次

• 而对于交换次数而言，当最好的情况下，交换为0次，最差的情况下，即逆序的情况，其交换次数为$n-1$次，基于最终的排序时间是比较次数+交换次数，因此，选择排序的时间复杂度为O(n^2)
• 一种不稳定的排序算法

测试代码：

#include <iostream>
#include <vector>
using namespace std;

void SelectSort(vector<int>& vec);
void PrintStep(vector<int> vec, int n, int i);
void PrintResult(vector<int> vec, int n);

void SelectSort(vector<int>& vec)
{
	cout << "--------------选择排序--------------" << endl;
	int n = vec.size();
	int minIndex;
	for (int i = 0; i < n - 1; ++i)
	{
		minIndex = i;
		for (int j = i + 1; j < vec.size(); ++j)
		{
			if (vec[j] < vec[minIndex])
				minIndex = j;
		}
		if (i != minIndex)
			swap(vec[i], vec[minIndex]);
		PrintStep(vec, n, i);
	}
	cout << "最终排序结果为：";
	PrintResult(vec, n);
}

void PrintStep(vector<int> vec, int n, int i)
{
	cout << "第" << i + 1 << "次排序结果： ";
	for (int j = 0; j < n; ++j)
		cout << vec[j] << ' ';
	cout << endl;
}

void PrintResult(vector<int> vec, int n)
{
	for (int j = 0; j < n; ++j)
		cout << vec[j] << ' ';
	cout << endl;
}
int main(int argc, char **argv)
{
	int a[] = {9,1,5,8,3,7,4,6,2};
	vector<int > vec(a, a+9);
	SelectSort(vec);
	return 0;
}