Numerical Optimization之信任域方法——Dogleg

上文中提到的近似柯西方向是延梯度方向下降一定步长，但是没有充分利用B矩阵，为此DOgleg 方法，当PB在信赖域中时利用PB，否则的话利用梯度方向下降一定步长，并且下降步长的计算方法也有所不同：
在柯西方法中是$\tau \Delta /||g||$，而Dogleg 中下降步长$a=-\frac{g^{T}g}{g^{T}Bg}$

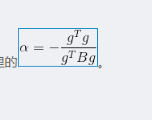
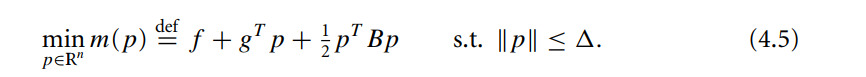
$P_k^B$是全局最优点，如果其在可行域当中的话，理所当然，我们应将它作为更新步


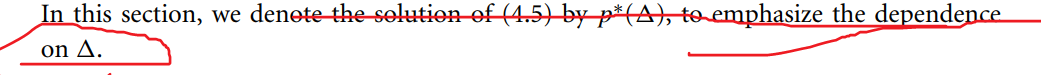
省支二次项后沿梯度方向下降最快，下降步长为$\Delta$



说明：令$f=x{g}^T+\frac{1}{2}{x}^{T}Bx$ 记$g=\frac{df}{dx}=g+B^{T}x$,可以计算出$P^U$

由引理知，当$P(\tau )$与信赖域相交时（），则取得最优的$P(\tau )$
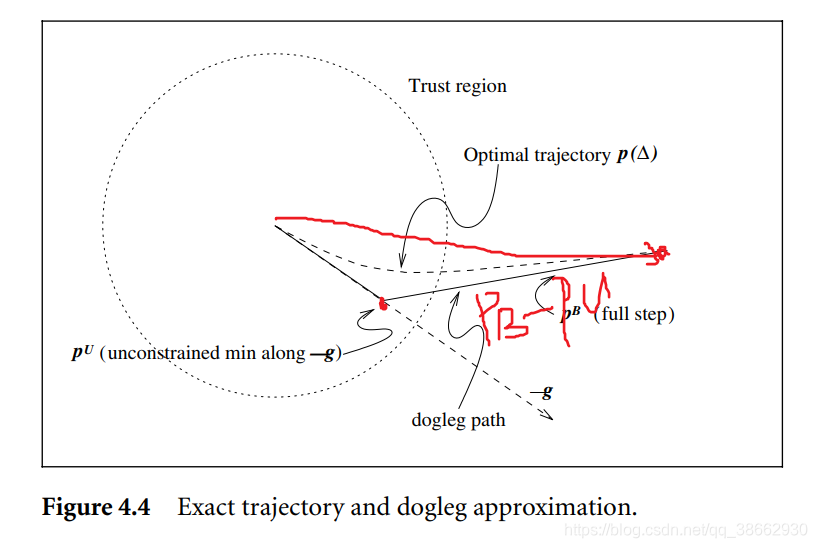
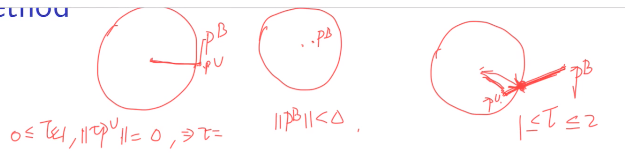
因此以下有三种情况：即PU在外部，PB在内部，PB在外部且PU在内部

部分来源于

拓展：二维子空间方法：即在$P^U$,$P^B$形成的子空间中，寻找最佳的P,
未知量是关于$\beta ,\alpha$,代入目标函数中，求出这两个变量便可以求出最佳的P，由于在空间中搜索，待定的P的选择性增多