神经网络是一种运算模型,由大量的节点(或称神经元)之间相互联接构成。每个节点代表一种特定的输出函数,称为激励函数(activation function)。每两个节点间的连接都代表一个对于通过该连接信号的加权值,称之为权重,这相当于人工神经网络的记忆。网络的输出则依网络的连接方式,权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近,也可能是对一种逻辑策略的表达。
以上来自百度百科的定义显得比较高冷,作为初学的入门者,我对其的理解是:
首先,神经网络的基础作用是分类既是识别,更高级的神奇功能也是在其之上建立的。而神经网络分为三层:输入层、隐藏层、输出层。结构决定功能,神经网络想要模拟人脑神经元作用机制,于是将输入层的信号通过一定处理,通过隐藏层(权重、偏置、激活函数)处理,得到输出信号既是输出层。
隐藏层的构架决定神经网络性能,因为隐藏层的构架实质是对实例的抽象,每一层关注实例的不同属性。
权重代表其对应前一层对后面神经元的影响;偏置决定神经元是否应该激活。
神经元是容器,容纳数字,代表本神经元的响应程度。
一、前向传播
前向传播(Forward propagation),在已知权重的情况下,得到分类结果的算法。
过程不用赘述。输入层有了,偏置值有了,自然可以得到下一层激活值,最终得到预测结果。
二、反向传播算法
(一)浅显了解
反向传播算法是建立在梯度下降基础之上的优化算法。所以可以了解的是,反向传播全程重要的一点是求误差函数对权重的偏导数、以及如何更快更省力地求误差函数对权重的偏导数。所以牢记这一点,防止被知识的洪水淹没。
(二)浅显实现步骤
首先要得到δ,一种中间参数,用于快速求偏导数。δl数目与神经元数目相等。但输入层对应的误差无太多意义,因为输入层到隐藏层第一层的参数偏导数由隐藏层第一层δ与输入层决定。也就是说第L层到第L+1层的权重偏导数由第L+1层δ与第L层激活值决定。而最后一层的δ由预测值与实际值决定。
1.计算最后一层也就是输出层δ:(实际值-预测值)*预测值*(1-预测值)。输出层有多少神经元就有多少δ。
2.倒数第二层到输出层的参数偏导数等于:输出层对应神经元δ*前一层激活值。
3.计算倒数第二层δ:设倒数第二层有j个神经元,每个神经元对输出层有k个映射,即有k个输出神经元,有k个参数。每个神经元的δ等于:权重*对应神经元δ,然后累加。
4.倒数第三层到倒数第二层的参数偏导数等于:倒数第二层对应神经元δ*前一层激活值。
5.以此类推,得到所有偏导数。
6.梯度下降更新参数,重复1-5.
(三)反向传播推导
反向传播的推导,其实本质是优化后的链式法则。
所以其根本是微积分链式法则求偏导。之所以是优化后,则是因为使用了中间参数δ消除重复计算。
那么如果直观思考,不使用中间参数,直接求偏导,会是什么样子的呐?
首先我们需要一个简单结构的神经网络作为说明。

首先,我们从前往后进行正向传播
netj=∑iwji∗oinet_j = \sum_i w_{ji}*o_inetj=∑iwji∗oi
oj=s(netj)(s为激活函数)o_j = s(net_j)(s为激活函数)oj=s(netj)(s为激活函数)
netk=∑jwkj∗ojnet_k = \sum_j w_{kj}*o_jnetk=∑jwkj∗oj
ok=s(netk)o_k = s(net_k)ok=s(netk)
经过这四步完成正向传播,得到预测值oko_kok,再通过实际值tkt_ktk得到误差函数
E=12∑k(tk−ok)2E = \frac{1}{2}\sum_k (t_k - o_k)^2E=21∑k(tk−ok)2
当然,这所有的一切只是在一个样本中,输入特征值,得到不同分类的概率。
接下来进行反向传播求偏导数。
- 假如我比较头铁,恰好我学过微积分的偏导数该怎么算,那我开始闷头算了
Δwkj=∂E∂ok∗∂ok∂netk∗∂netk∂wkj=∂E∂ok∗∂ok∂netk∗oj\Delta w_{kj} = \frac{\partial E}{\partial o_k} *\frac{\partial o_k}{\partial net_k}*\frac{\partial net_k}{\partial w_{kj}} = \frac{\partial E}{\partial o_k} *\frac{\partial o_k}{\partial net_k}*o_jΔwkj=∂ok∂E∗∂netk∂ok∗∂wkj∂netk=∂ok∂E∗∂netk∂ok∗oj
这一层我需要算三次导数。
下一层:
Δwji=∑k∂E∂ok∗∂ok∂netk∗∂netk∂oj∗∂oj∂netj∗∂netj∂wji\Delta w_{ji} =\sum_k \frac{\partial E}{\partial o_k} *\frac{\partial o_k}{\partial net_k}*\frac{\partial net_k}{\partial o_{j}}* \frac{\partial o_j}{\partial net_j}* \frac{\partial net_j}{\partial w_{ji}}Δwji=∑k∂ok∂E∗∂netk∂ok∗∂oj∂netk∗∂netj∂oj∗∂wji∂netj
这一层的求导实际要求五层导,因为wjiw_{ji}wji实际影响了所有输出,所以还要累加所有路径的偏导数(我忘了这叫什么求导,对不起我的微积分老师)。 - 我头痛地发现这样算太繁琐,计算量太大了,所以我观察了一下式子,发现有重复计算的现象。
哪里重复了呐?
∂E∂netk\frac{\partial E}{\partial net_k}∂netk∂E
我们想一下,wkjw_{kj}wkj实际可以换一种形式
Δwkj=∂E∂netk∗∂netk∂wkj\Delta w_{kj} = \frac{\partial E}{\partial net_k} *\frac{\partial net_k}{\partial w_{kj}}Δwkj=∂netk∂E∗∂wkj∂netk
同理
Δwij=∂E∂netj∗∂netj∂wji\Delta w_{ij} = \frac{\partial E}{\partial net_j} *\frac{\partial net_j}{\partial w_{ji}}Δwij=∂netj∂E∗∂wji∂netj
而∂E∂netj\frac{\partial E}{\partial net_j}∂netj∂E的计算与∂E∂netk\frac{\partial E}{\partial net_k}∂netk∂E有直接关系。推导如下:
∂E∂netk=∂E∂oj∗∂oj∂netj=∂E∂oj∗oj(1−oj)=(∑k∂E∂netk∗∂netk∂oj∗)oj(1−oj)=(∑k∂E∂netk∗wkj)∗oj(1−oj)\frac{\partial E}{\partial net_k} =\frac{\partial E}{\partial o_j}*\frac{\partial o_j}{\partial net_j}=\frac{\partial E}{\partial o_j}*o_j(1-o_j)=(\sum_k\frac{\partial E}{\partial net_k}*\frac{\partial net_k}{\partial o_j}*)o_j(1-o_j)=(\sum_k\frac{\partial E}{\partial net_k}*w_{kj})*o_j(1-o_j)∂netk∂E=∂oj∂E∗∂netj∂oj=∂oj∂E∗oj(1−oj)=(∑k∂netk∂E∗∂oj∂netk∗)oj(1−oj)=(∑k∂netk∂E∗wkj)∗oj(1−oj)
所以基本就可以结束了,误差函数对每一层激活值的导数,就是所谓的中间参数δ。而δ是可以用层层传递的方式,减少计算量。就其本质而言,则是误差的层层传递。
只要计算了最后一层∂E∂netk\frac{\partial E}{\partial net_k}∂netk∂E,就可以得出最后一层的偏导数,以及上一层的∂E∂netj\frac{\partial E}{\partial net_j}∂netj∂E,以此层层类推,得出所有层的δ以及偏导数。
有了偏导数,就可以对参数进行梯度下降优化了。
以下给出含δ的推导过程

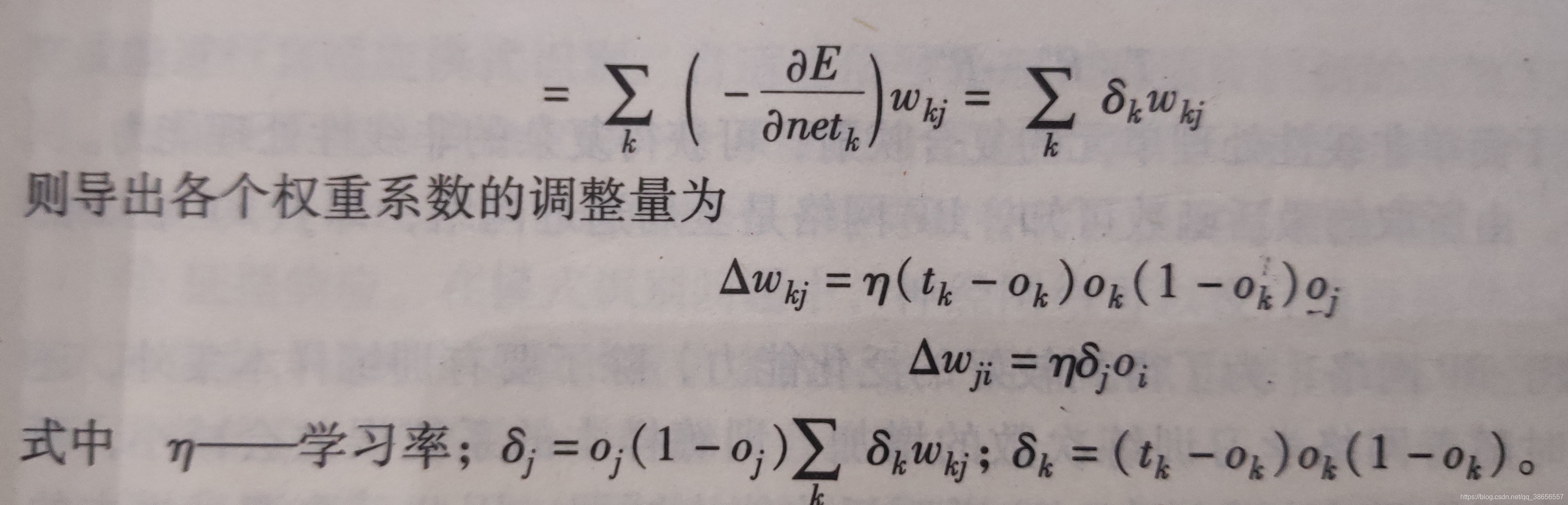
(完)
ps:部分内容来源网络及图书,如涉侵权,请联系作者。








 本文是吴恩达机器学习课程的个人总结,重点介绍了神经网络的结构和功能,特别是前向传播和反向传播算法。前向传播用于根据权重获取分类结果,而反向传播基于梯度下降优化权重,通过δ参数简化偏导数计算,实现误差的层层传递,以优化网络性能。
本文是吴恩达机器学习课程的个人总结,重点介绍了神经网络的结构和功能,特别是前向传播和反向传播算法。前向传播用于根据权重获取分类结果,而反向传播基于梯度下降优化权重,通过δ参数简化偏导数计算,实现误差的层层传递,以优化网络性能。
















 9591
9591

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








