数字图像处理（二）——边缘检测

边缘是图像中灰度发生急剧变化的区域边界，图像灰度的变化情况可以用灰度分布的梯度来表示，数字图像中求导是利用差分近似微分来进行的，实际上常用空域微分算子通过卷积来完成。

1 一阶导数算子

1.1 Roberts

Roberts算子是一种斜向偏差分的梯度计算方法，梯度的大小代表边缘的强度，梯度的方向与边缘的走向垂直。Roberts操作实际上是求旋转45度两个方向上微分值的和。Roberts算子定位精度高，在水平和垂直方向的效果好，但对噪声敏感。两个卷积核Gx、Gy分别为：

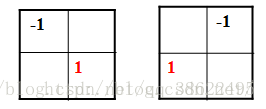
采用1范数衡量梯度的幅度为：

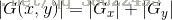
1.2 Sobel

Sobel算子是一组方向算子，从不同的方向检测边缘。Sobel算子不是简单的求平均再差分，而是加强了中心像素上下左右4个方向像素的权值，运算结果是一副边缘图。Sobel算子通常对灰度渐变和噪声较多的图像处理的比较好。两个卷积核Gx、Gy分别为：

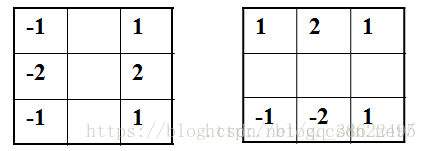
采用范数衡量梯度的幅度为：

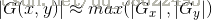
1.3 prewitt

Prewitt算子是一种边缘样板算子，利用像素点上下左右邻点灰度差，在边缘处达到极值检测边缘，对噪声具有平滑的作用。由于边缘点像素的灰度值与其邻域点的灰度值显著不同，在实际应用中通常采用微分算子和模板匹配的方法检测图像的边缘。Prewitt算子不仅能检测边缘点，而且能抑制噪声的影响，因此对灰度和噪声较多的图像处理得比较好。两个卷积核Gx、Gy分别为：

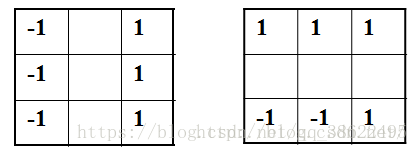
采用范数衡量梯度的幅度为：

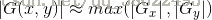
2 二阶导数算子

也可以检测边缘，利用二阶导数算子检测阶梯状边缘需将检测算子与图像卷积并确定过零点。

2.1 Laplacian

Laplacian 根据二阶导数算子过零点的性质来确定边缘的位置。
Laplacian模板：对应中心像素和邻近像素的系数的和是零。

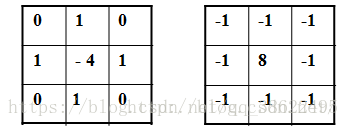
拉普拉斯算子检测方法常常产生双像素边界，而且这个检测方法对图像中的噪声相当敏感，不能检测边缘的方向，所以很少直接使用拉普拉斯算子进行边缘检测。

2.2 马尔

马尔算子是在Laplacian算子的基础上实现的。Laplacian算子对噪声比较敏感，为了减少噪声的影响，可先对图像进行平滑然后再运用Laplacian算子。由于成像时，一个给定的像素点所对应场景点的周围对该点的光强贡献呈高斯分布，所以所进行平滑的函数可以采用高斯加权平滑函数。

拉普拉斯算子与高斯滤波结合在一起，形成LOG算子，也成为拉普拉斯-高斯(Laplacian-Gauss)算子。LOG算子是对Laplacian算子的改进，他需要考虑5*5邻域的处理，从而获得更好的检测效果。
马尔算子的计算如下：

• 用一个2-D的高斯平滑模板与原图像卷积

• 计算卷积后拉普拉斯值。

• 检测拉普拉斯图像的过零点作为边缘点。

2.3 Canny

Canny算子把边缘检测问题转换为检测单位函数极大值的问题来考虑。他利用高斯模型，借助图像滤波的概念指出一个好的边缘检测算子应该具有3个指标：

• 低失误率，既要少将真的边缘丢弃，也要少将非边缘判为边缘；（信噪比准则）

• 高位置精度，检测出的边缘应在真正的边界上；（定位精度准则）

• 单像素边缘，即对每个边缘有唯一的响应，得到的边界为单像素宽。（单边缘响应准则）

2.3.1 信噪比准则

信噪比越大，提取的边缘质量越高。信噪比SNR定义为：

其中，G(x)代表边缘函数，h(x)代表宽度为W的滤波器的脉冲响应。

2.3.2 定位精度准则

边缘定位的精度L定义如下：

其中，G’(x)和h’(x)分别是G(x)和h(x)的导数。L越大表明定位精度越高。

2.3.3 单边缘响应准则

为了保证单边缘只有一个响应，检测算子的脉冲响应导数的零交叉点的平均距离D(f’)应满足：

满足上述三个条件的算子称为Canny算子。Canny边缘检测算法的步骤如下:

• 用高斯滤波器平滑图像；（简单来说就是使用Guess模板在原始图像中进行移位、相乘、相加的过程。）

• 用一阶偏导的有限差分来计算梯度图像的边缘幅值与角度；(计算图像梯度可以选择算子有Robot算子、Sobel算子、Prewitt算子等。)
  根据x方向和y方向的卷积模板，可知，在3×3邻域中从底部一行像素值减去顶部一行的像素，得到x方向的偏导数(梯度)；同样，从右边一列像素值减去左边一列的像素，得到y方向的偏导数。 (prewitt)
  x方向的梯度： $g_x=∂f/∂x=(0−0)+(0−1)+(0−1)=−2$
  y方向的梯度： gy=∂f/∂x=(1−0)+