#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cmath>
using namespace std;
const int maxn = 1e5 + 10;
int a[maxn];
vector<int> G[maxn];
int T;
int n, m;
void process(int x, int loc)
{
int t = (int)sqrt(x);
for(int i = 2; i <= t; i++)
{
while(x % i == 0)
{
G[i].push_back(loc);
x /= i;
}
}
if(x > 1)
G[x].push_back(loc);
}
int main()
{
cin >> T;
while(T--)
{
for(int i = 1; i < maxn; i++)
G[i].clear();
cin >> n >> m;
int t;
for(int i = 1; i <= n; i++)
{
scanf("%d", &t);
process(t, i);
}
int l, r, x;
for(int i = 1; i <= m; i++)
{
scanf("%d%d%d", &l, &r, &x);
int tt = (int)sqrt(x);
int cnt;
bool flag = true;
for(int j = 2; j <= tt; j++)
{
cnt = 0;
while(x % j == 0)
{
cnt++;
x /= j;
}
if(!cnt) continue; //每次边拆分边判断,就不需要再开数组存查询的质因数分解并比较,简便。
//int dif = upper_bound(G[j].begin(), G[j].end(), r) - pos - (lower_bound(G[j].begin(), G[j].end(), l) - pos); 完整理解,-pos + pos抵消
int dif = upper_bound(G[j].begin(), G[j].end(), r) - lower_bound(G[j].begin(), G[j].end(), l);
if(dif < cnt)
{
flag = false;
break;
}
}
if(x > 1) //注意千万记得特判 > sqrt(x)的质因数,坑点!
{
int dif = upper_bound(G[x].begin(), G[x].end(), r) - lower_bound(G[x].begin(), G[x].end(), l);
if(dif < 1)
{
flag = false;
}
}
if(flag)
printf("Yes\n");
else
printf("No\n");
}
}
return 0;
}







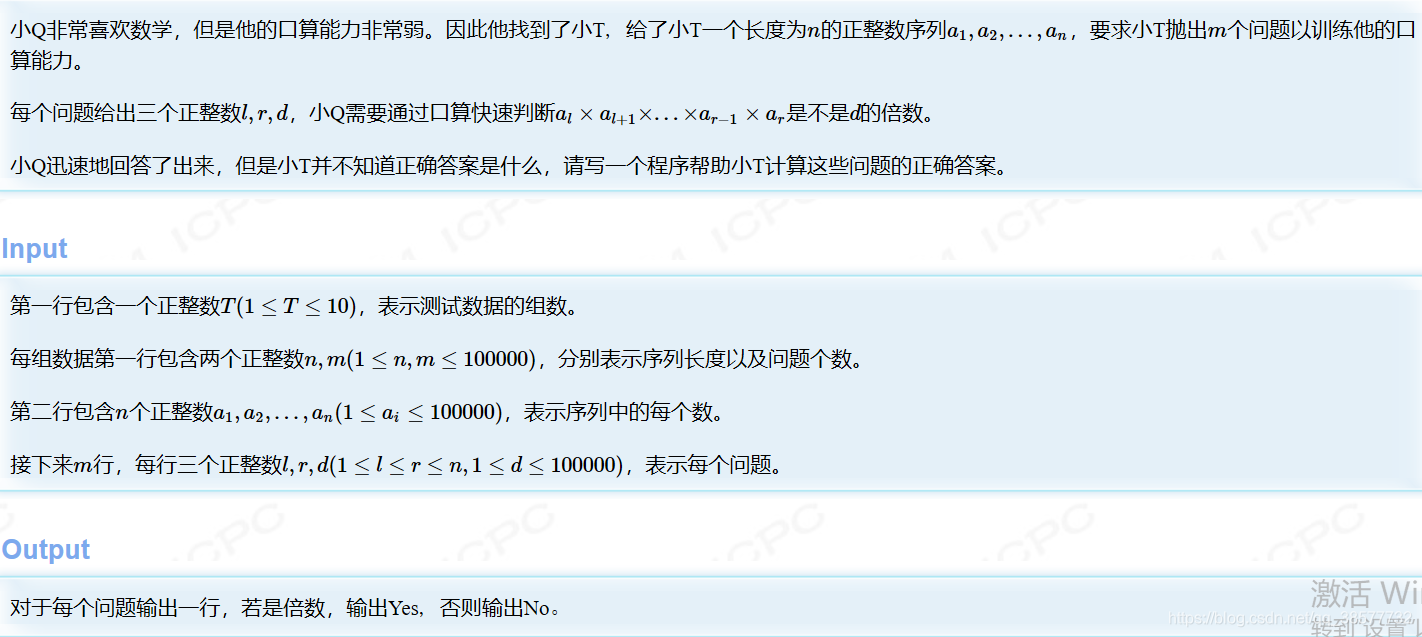
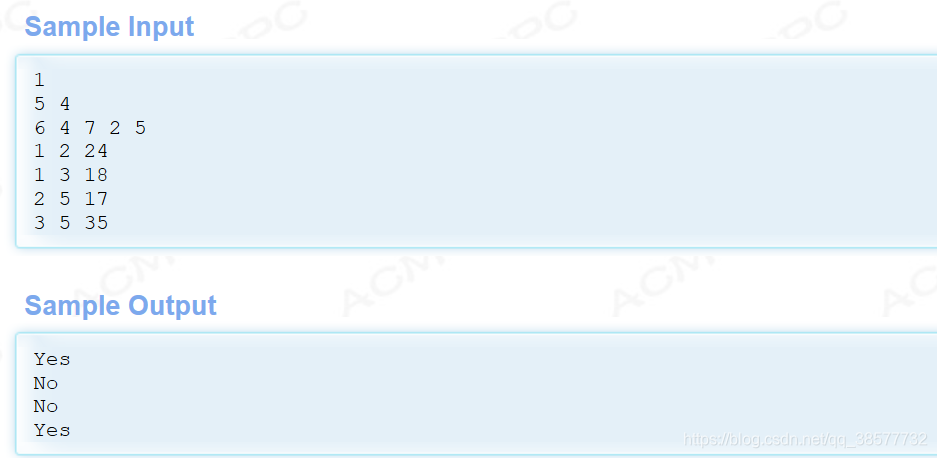
 博客围绕hdu6287展开,涉及思维相关内容,但因内容缺失,具体关键信息不明。
博客围绕hdu6287展开,涉及思维相关内容,但因内容缺失,具体关键信息不明。
















 453
453

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








