机器篇——线性回归 公式 图文 代码 相互结合详细讲解

一.线性回归的相关理论

   1.回归

         大自然总是让我们回归到一定的区间之内。就好像，除了少数的伟人，我们绝大部分人会回归到平凡，成人普通人。而那些伟人很少，普通民众很多，整体分布就类似于正态分布图一样。这，也是我们回归的分布图。

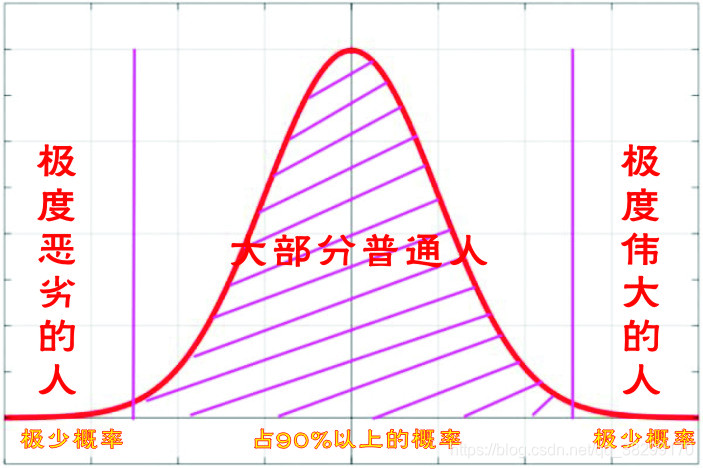
          在英雄的传记里面，英雄往往就那么几个人，而整个世界，基本是普通人。这，也是绝大部分人，都会被回归普通，回归平凡，那些英雄只是特例。

         

   2.中心极限定理

         (1).概率论中讨论随机变量序列部分和分布逐近于正态分布的一类定理

         (2).这组定理是数理统计学和误差分析的理论基础，指出了大量随机变量累积分布函数逐点收敛到正态分布的积累分布函数的条件

         (3).在自然界与生产中，一些现象受到许多相互独立的随机因素的影响，如果每个因素所产生的影响都很微小时，总的影响可以看作使你服从正态分布的。

 

   3.最大似然估计

         (1).最大似然估计是一种统计学方法，它用来求一个样本集的相关概率密度函数的参数。

         (2).最大似然估计法明确的使用概率模型，其目标是寻找能够以较高概率产生观察数据的系统发生树。

         (3).最大似然函数:

                a.总体x为离散型时:(离散型，就用概率的方法算)

                       

                     

                        

                b.总体x为连续型时:(连续型，就用积分的方法算)

                     

                     

                      

        (4).对数似然函数:

              对似然函数两边取对数，对 lnL(θ) 求导，并令之为0: 

                     

                         

             解对数似然方程所得，即为未知参数的最大似然估计值。

 

   4.概率密度函数

        (1).在数学中，连续型随机变量的概率密度函数是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。

        (2).而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。

        (3).正太分布是重要的概率分布，它的概率密度函数是:

                   

                    ：为正太分布中的误差期望，误差期望值越小越好，最好为0.

                    ：为误差值，，为真实值，为预测值，等价于，即 

                    ：为标准差，:为方差

                    当  时：

                   

               

   5.从最大似然估计到采样的最大可能性

       给定一个概率分布D，已知其概率密度函数(连续分布)，或概率质量函数(离散分布)为，以及一个分布参数θ，可以从这个分布中抽出具体n个值的采样，，........，利用计算出其似然函数:

              

       (1).若D是离散分布，即是在参数为θ时观测到这一采样的概率

       (2).若D是连续分布，则为，，........联合分布的概率密度函数在观测值处的取值。

       (3).一旦获得，，........，就能求得一个关于θ的估计。最大似然估计会寻找关于θ的最可能的值(即，在所有可能的θ值中，寻找到一个值，使得这个采样的“可能性”最大化)。

       (4).这个使可能性最大的θ值，即称为最大似然估计。

 

   注意：

            给出上面这些概念，是因为，接下来要讲的线性回归，是服从正太分布，服从中心极限定理，服从最大似然估计的。这，就是为什么，在线性回归中，需要用正态分布的概率密度函数。因为，如果不服从上面这些理论，就没办法用下面的线性回归。上面的定理，是前提。

 

二.线性回归

   1.一元线性回归:

       当只有一个因素(特征)的时候:

                

       也就是二维空间中的一条直线

 

   2.多元线性回归:

       当不止一个因素(特征)的时候:

              

       也就是高维空间中的一条直线

       (1).在机器学习中一般写成：

               

              因为一般规定  = 1，所以上式一般写成:

              

               通过式子计算出来的 为 预测值，真实的 为真实值。

       (2).令  ,    

              则

                        

             所以有：    

                    

       (3).误差 ：

                

               

 

   3.线性回归的目标函数求解:

       (1).将线性回归的误差带入到线性回归的正太分布概率密度函数中，有:

               

              

       (2).根据最大似然求概率函数: 

              

                                   

       (3).目标函数