word2vec是用来生成词向量的相关模型,由Google在2013年提出,相关的论文有以下三篇
Efficient Estimation of Word Representations in Vector Space
Distributed Representations of Words and Phrases and their Compositionality
基本介绍
word2vec的基本思想是:利用相似的词具有相似的上下文这一思想,训练神经网络模型。模型的输入是某个词,输出是这个词的上下文。经过神经网络的训练后,可以得到每一个词在高维空间中的向量表示,其中相似的词语在高维空间中的向量表示也是相互靠近的。
word2vec有两种不同的模型,分别是CBOW和Skip-Gram.CBOW的基本思想是:用上下文词来预测中心词;Skip-Gram的基本思想是:用中心词来预测上下文词。
1.背景知识
在word2vec提出前,已经有很多表示词向量的方法,也有一些神经网络语言模型。但是这些模型或多或少会存在一定的缺陷。
1.1词向量
词向量的表示分为离散型和分布式型两种,离散型的词向量表示,词语与词语之间没有直接的联系,无法计算不同词向量之间的相似性;分布式型的词向量有传统的n-gram模型以及神经网络语言模型,分布式的词向量之间的关系可以进行计算。
1.1.1 one-hot
one-hot是最简单的词向量表示,它的形式是用N维向量来表示单词(N代表词表的长度),在N维向量中,单词对应词表的序号维度上的值为1,其余都为0.这种编码方式存在很多缺陷。
1.1.2词袋模型
词袋模型的维度也是N,与one-hot不同的是,词袋模型的词向量中每一个维度的数值都代表词表中的单词在文本中出现的次数。这种方式也存在很多缺陷。
1.2 语言模型
神经网络语言模型用来训练词向量,它可以获得分布式的词向量,这种词向量解决了离散型词向量的缺陷。
1.2.1n-gram模型
1.2.2NNLM
参考论文《A Neural Probabilistic Language Model》
2.word2vec模型
word2vec有两种模型,分别是CBOW和Skip-Gram,下边分别介绍这两种模型的基本架构。
2.1 CBOW模型
CBOW模型是指,在已知一个单词上下文的情况下,对这个单词进行预测。例如已知单词
w
t
−
2
,
w
t
−
1
,
w
t
+
1
,
w
t
+
2
w_{t-2},w_{t-1},w_{t+1},w_{t+2}
wt−2,wt−1,wt+1,wt+2,预测单词
w
t
w_t
wt.学习的目标是最大化对数似然函数
∑
l
o
g
p
(
w
∣
C
o
n
t
e
x
t
(
w
)
)
\sum logp(w|Context(w))
∑logp(w∣Context(w))
CBOW的模型架构图如下

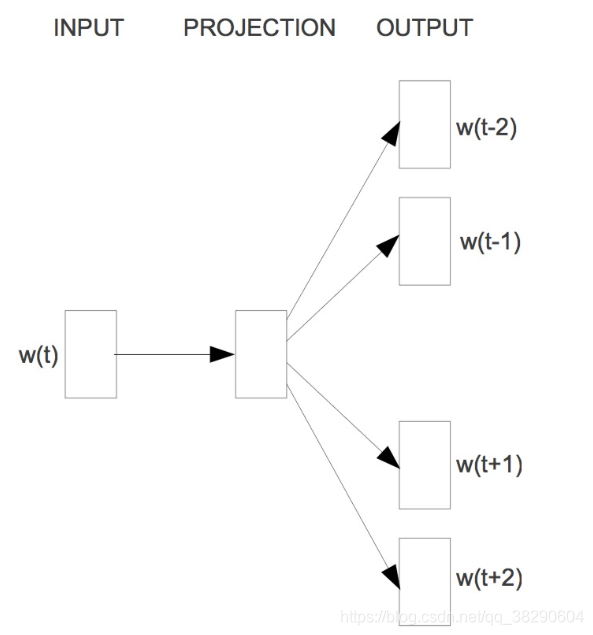
2.2 skip-gram模型
skip-gram模型是指,在已知上下文的情况下,对中心词进行预测。例如已知单词
w
t
w_t
wt,预测上下文单词
w
t
−
2
,
w
t
−
1
,
w
t
+
1
,
w
t
+
2
w_{t-2},w_{t-1},w_{t+1},w_{t+2}
wt−2,wt−1,wt+1,wt+2.学习的目标函数是
∑
l
o
g
p
(
C
o
n
t
e
x
t
(
w
)
∣
w
)
\sum logp(Context(w)|w)
∑logp(Context(w)∣w)
skip-gram的模型架构图如下
3 word2vec的基本策略
3.1 Hierarchical Softmax
word2vec的两种模型中,从隐藏层到输出之间需要经过softmax的计算,最后才能得模型 的概率输出。但是传统的softmax的计算复杂度很高,计算复杂度为
O
(
V
)
O(V)
O(V),V是词表长度。使用Hierarchical Softmax计算可以将模型的计算复杂度降低到
O
(
l
o
g
2
V
)
O(log_2V)
O(log2V).
传统的softmax会对神经网络的每一个输出节点计算其概率分布,而hierarchical softmax不需要计算所有的节点,它使用了二叉树的结构来表示词典中的所有词。
3.1.1 二叉树的构建
hierarchical sofmax构建的二叉树中,叶子节点是词表中的每一个单词。假设词表有
V
V
V个单词,那么二叉树共有
V
V
V个叶子节点,
V
−
1
V-1
V−1个非叶子节点;对于每一个叶子节点(也就是词表中的单词),都有一个从根节点出发到该节点的唯一路径。根节点到叶子节点所走的路径,就是求该叶子节点出现概率的计算路径。

hierarchical softmax的二叉树是按照概率进行路径选择的。采用了二元逻辑回归的方法,即规定沿着左子树走,那么就是负类(霍夫曼树编码1),沿着右子树走,那么就是正类(霍夫曼树编码0)。判别正类和负类的方法是使用sigmoid函数,即:
P
(
+
)
=
σ
(
x
w
T
θ
)
=
1
1
+
e
−
x
w
T
θ
P(+)=σ(x^T_wθ)=\frac{1}{1+e^{-x^T_wθ}}
P(+)=σ(xwTθ)=1+e−xwTθ1其中
x
w
x_w
xw是当前内部节点的词向量,而θ则是我们需要从训练样本求出的逻辑回归的模型参数。同理可得,
P
(
−
)
=
1
−
P
(
+
)
P(−)=1−P(+)
P(−)=1−P(+).
P
(
−
)
=
1
−
σ
(
x
w
T
θ
)
=
1
−
1
1
+
e
−
x
w
T
θ
P(-)=1-σ(x^T_wθ)=1-\frac{1}{1+e^{-x^T_wθ}}
P(−)=1−σ(xwTθ)=1−1+e−xwTθ1在路径选择的时候,对于向左走还是向右走要对比
P
(
+
)
P(+)
P(+)和
P
(
−
)
P(-)
P(−)的大小,若
P
(
−
)
P(-)
P(−)大于
P
(
+
)
P(+)
P(+),那么就想左走,反之向右走。
3.1.2 目标函数
以上图从根节点走到
w
2
w_2
w2节点为例进行目标函数的计算,从图中深颜色的路径来看,模型一共进行了三次选择,即从
n
(
w
2
,
1
)
n(w_2,1)
n(w2,1)到
n
(
w
2
,
2
)
n(w_2,2)
n(w2,2),从
n
(
w
2
,
2
)
n(w_2,2)
n(w2,2)到
n
(
w
2
,
3
)
n(w_2,3)
n(w2,3),从
n
(
w
2
,
3
)
n(w_2,3)
n(w2,3)到
w
2
w_2
w2,走到节点
w
2
w_2
w2的概率等于这三次每一次选择的概率。所以上图的搜索过程的目标函数为
∏
i
=
1
3
P
(
n
(
w
i
)
,
i
)
=
(
1
−
1
1
+
e
−
x
w
T
θ
1
)
(
1
−
1
1
+
e
−
x
w
T
θ
2
)
(
1
1
+
e
−
x
w
T
θ
3
)
\prod_{i=1}^{3} P(n(w_i),i)=(1-\frac{1}{1+e^{-x^T_wθ_1}})(1-\frac{1}{1+e^{-x^T_wθ_2}})(\frac{1}{1+e^{-x^T_wθ_3}})
i=1∏3P(n(wi),i)=(1−1+e−xwTθ11)(1−1+e−xwTθ21)(1+e−xwTθ31)
为了便于我们后面一般化的描述,我们定义输入的词为
w
w
w,其从输入层词向量求和平均后的霍夫曼树根节点词向量为
x
w
x_w
xw, 从根节点到
w
w
w所在的叶子节点,包含的节点总数为
l
w
lw
lw,
w
w
w在霍夫曼树中从根节点开始,经过的第
i
i
i个节点表示为
p
i
w
p_i^w
piw,对应的霍夫曼编码为
d
i
w
∈
(
0
,
1
)
d_i^w∈(0,1)
diw∈(0,1),其中
i
=
2
,
3
,
.
.
.
l
w
i=2,3,...l_w
i=2,3,...lw。而该节点对应的模型参数表示为
θ
i
w
θ^w_i
θiw, 其中
i
=
1
,
2
,
.
.
.
l
w
−
1
i=1,2,...l_{w−1}
i=1,2,...lw−1.
定义
w
w
w经过某个节点
j
j
j的逻辑回归概率为

那么对于某一个目标输出词
w
w
w,其最大似然为:

参数更新公式:
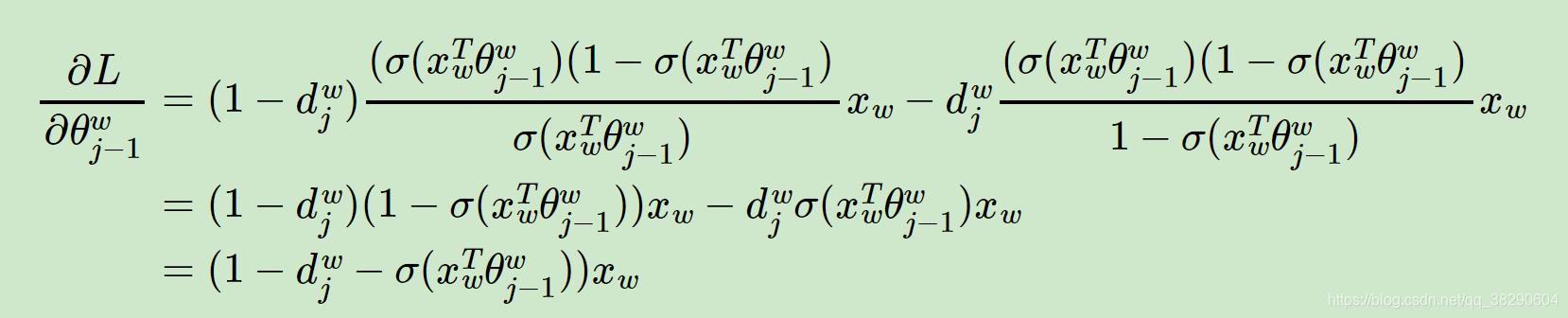

参考
word2vec原理(二) 基于Hierarchical Softmax的模型
关于word2vec的一些相关问题整理 & 思考
Word2Vec原理之层次Softmax算法








 本文介绍了word2vec模型,包括词向量的基础,如one-hot和词袋模型,以及word2vec的两种模型CBOW和Skip-Gram。重点讲述了Hierarchical Softmax策略,用于降低计算复杂度,并详细解析了二叉树的构建和目标函数计算。
本文介绍了word2vec模型,包括词向量的基础,如one-hot和词袋模型,以及word2vec的两种模型CBOW和Skip-Gram。重点讲述了Hierarchical Softmax策略,用于降低计算复杂度,并详细解析了二叉树的构建和目标函数计算。
















 2127
2127

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








