生成树算法求解网络容量最大连通图

问题描述

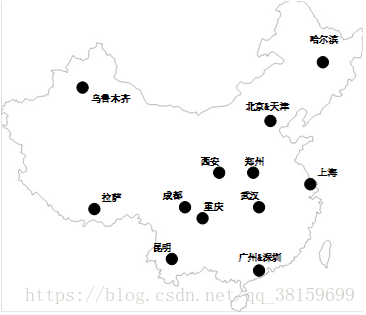
图一

单波传输容量	最大传输距离	总容量
100 Gb/s	3000 km	8 Tb/s
200 Gb/s	1200 km	16 Tb/s
400 Gb/s	600 km	32 Tb/s

表1 不同传输格式的传输距离

现有12个城市之间进行通信，考虑到通信网络的目的是把更多的人更充分地连接到一起，我们按照如下方式定义网络的价值。

每条直接连接两个城市/区域的链路当做1个连接，每个连接的价值定义为传输的容量与连接区域人口数的乘积（取两区域人口数乘积的0.5次方）每条直接连接两个城市/区域的链路当做1个连接，每个连接的价值定义为传输的容量与连接区域人口数的乘积（取两区域人口数乘积的0.5次方）。

网络的价值则是所有连接价值的加权和网络的价值则是所有连接价值的加权和：

网络价值=∑权重*容量*人口

此题中权重默认为1，容量和距离有关，计算方法如表一所示。其中两城市间距离由经纬度求出。

问题：如果连接数从16增加到33条时，不考虑中间节点，给出你们的两个网络规划及其价值。网络价值最多是多少？

图相关概念

连通图：在无向图中，若任意两个顶点vi与vj都有路径相通，则称该无向图为连通图。

生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。

最大生成树：参照最小生成树的定义，与之相反，在连通网的所有生成树中，所有边的代价和最大的生成树，称为最大生成树。

最大生成树prim算法

要满足所有城市之间都有直接或间接的连接，需要得到连通图。因此，可以将城市两两直接连接的价值量视作树枝的权值，用prim算法求出最大生成树。

考虑到要将所有城市连接，将12个城市相连通最少需11条连线，

我们在求出11条连接的最小生成树的基础上，再加上剩余的网络中价值量最大的5条（共16条连接）和22条（共33条连接），即可得到总网络价值量最大的网络连接方案。

最大生成树算法，需要先求出网络价值矩阵，如下所示：

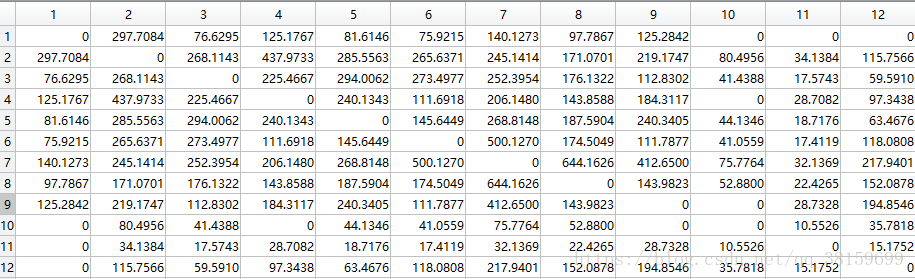
最小生成树及prim算法如链接所示 图–生成树和最小生成树。

需要注意的是，求解网络容量最大的连通图要每次取与已有节点相连的节点中连接价值量最大的新节点。
[1]: http://www.ximizi.com/jingweidu.php

城市经纬度查询