树

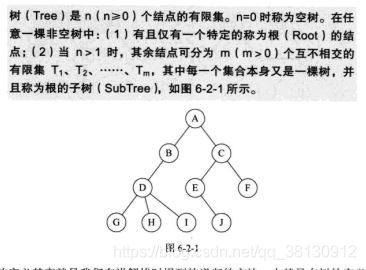
树定义强调：
（1）n>0时，根节点是唯一的。
（2）m>0时，子树的个数没有限制，但一定互补相交。
度（Degree）：结点拥有的子树数
叶结点：度为零的结点
分支结点：度不为零
树的度：度内各结点的度的最大值。
树的深度：树中结点的最大层次
无序树：将树中各子树看成从左到右是有序的，若不能交换的。
森林：m(m>=0)颗树互不相交的树的集合。
二叉树：

一、特点：
（1）每个结点最多有两颗子树。
（2）左子树和右子树是有顺序的，次序不能颠倒。
（3）即使树中只有一棵子树，也可以区分。
二、五种基本形态：
1、空二叉树
2、只有一个根结点
3、根结点只有左子树
4、根结点只有右子树
5、根结点有左子树和右子树
三、特殊二叉树：
斜树、满二叉树、完全二叉树
斜树：左斜树、友斜树
满二叉树：除叶子结点外，每个结点都有左右子树。
完全二叉树：

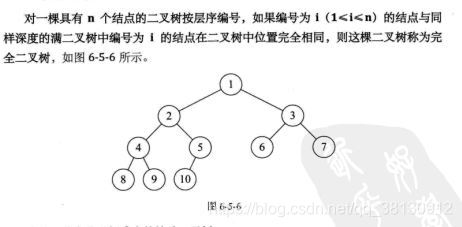
完全二叉树不一定是满的，而满二叉树一定是一颗完全的二叉树。
【重点】二叉树性质 5
1、二叉树的第i层至多有2^（i-1）个结点
2、深度为k的二叉树之多有2^k-1个结点
3、终端节点数No，度为2的结点树为Nz，
则No=Nz-1
4、具有n个结点的完全二叉树的深度为
L（log2^n） +1（L(x)表示不大于x的最大整数）
5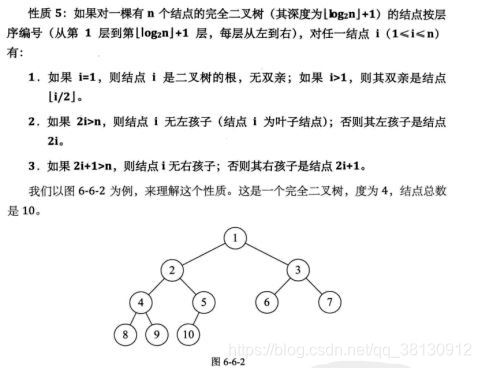
5·对应的问题
i=1 根结点
i>1 双亲结点 (i/2)
2i>n i无左孩子；否则左孩子是结点2i
2i+1>n i无右孩子，否则右孩子是结点2i+1
总结：
/ /二叉树性质：
//普通的1\2\3 二叉树第i层最多有2^(i-1)个结点
// 二叉树深度为k，最多有2^k-1结点
// 终端结点数等于度为2的结点数减一。
//完全二叉树45
// n个结点二叉树的深度为(log2^n)+1
// i=1 根节点
// i>1, i/2
// 2i>n 无左结点或者左结点为2i
// 2i+1>n
森林：m(m>=0)颗树互不相交的树的集合。
6、遍历二叉树：
前序遍历（从根出发，左子树、右子树）
中序遍历（左叶子结点出发 )
后序遍历（左叶子结点出发）
对应题目有：给中序遍历和其中另外一个遍历的序号，让求另外一个遍历的顺序。
解法： 先求出这棵树，然后再求另外一个遍历。
7、树、森林与二叉树的相互转换：
①树转二叉树：
三步走：
加线：给所有兄弟结点之间加一条连线；
去线：只保留树的每个结点与第一个孩子的连线，删除该结点与其他子的连线。
层次调整：以树根节点为轴心，将整个树顺时针旋转，规则为第一个孩子做二叉树的左孩子，兄弟转换为左孩子的右孩子。二叉树转树变为 加线、去线、调整。
②森林转化二叉树
两步走：
1、将每个树转化为二叉树；
2、第一棵树不动，第二颗树开始，依次把后一棵二叉树的根节点作为前一棵树的根的右孩子，用线连起来。
8、树和森林的遍历：
树 分为先根遍历、后根遍历
森林分为 前序遍历、 后序遍历
层次优先遍历用队列，深度优先用栈。
9、哈弗曼编码：
串：1234532143
出现数字 ：出现的频率
1：2
2：2
3：3
4：2
5：1
然后用最小的两个数做二叉树的叶结点即
11
7 3
5 2
3 4
5 1
然后给左子树赋0值，右子树赋1值，即可得到：
数：编码
5：0000
1：0001
4：001
2：01
1：1
即可以用相应的编码表示上面的串
。