假设函数、损失函数、 成本函数

基本概念

假设函数：假设函数用 h_θ 表示，并且使用我们选择的模型。对于一个输入数据 x⁽ⁱ⁾，模型预测输出为 h_θ(x⁽ⁱ⁾)

损失函数：用 L 表示。 将对应于真实数据 y 的预测值 z(h_θ) 作为输入，输出 y 与 z 之间的差异。所求的是单个样本之
                  间的差异

成本函数：用 J 表示。经常用于评估一个模型的性能，是损失函数对于整个样本数据的求和。

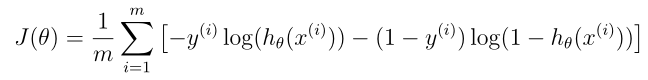
上图中，中括号内i = 1，2，3…m 时，就是损失函数，对其求和除以 m 得出成本函数。

因此成本函数和损失函数是两个不同的概念，虽然不是重要的知识，但还是要分清。

公式

因为在机器学习中，一般都是向量的计算，很少用 for 循环进行单个样本间的计算 (计算效率太低) ，所以图中并没有添加损失函数，了解一下就好。对于单个样本间的计算，我会在下一节梯度下降算法中详细解释。