MarkDown语句
下划线 <u>
text
<u>text
加粗 **
text
text
<b>text
*text*
斜体 _
斜体 or 斜体
*斜体* or _斜体_
加粗斜体
***加粗斜体***
一 ~ 六级标题
#~######
高亮 ==
text
==text==
删除线 ~~
删除线~~删除线~~
上标 ^
Ttext
T^text^
下标 ~
Ttext
T~text~
有序列表
- text
无序列表 -/+/*
-/+/* text
任务列表
- text
- [ ] text : 未完成
- text
- [x] text : 已完成
超链接
[text](url)
图片
! [img] (url)
引用
>
表格
| 表头1 | 表头2 |
|---|---|
|表头1|表头2|
公式块
$$
$$
代码块
import pandas as pd
```python
Latex 数学公式
希腊字母

δ,λΔ,Λαβϕ,φϵ,επ
\delta,\lambda \\
\Delta,\Lambda \\
\alpha\beta \\
\phi,\varphi\\
\epsilon,\varepsilon \\
\pi
δ,λΔ,Λαβϕ,φϵ,επ

\\: 换行
上下标

a2,b1xy+z,pij,pij
a^2,b_1\\
x^{y+z},p_{ij},p_ij
a2,b1xy+z,pij,pij
英文字母只有在表示变量时,才可使用斜体(默认),其余情况都应使用直立体(罗马体)
KaTeX parse error: Got function '\rm' with no arguments as subscript at position 29: …,...,n,为变量\\ x_\̲r̲m̲ ̲i :\rm i 表示“输入”…

直立体
| 罗马体 | 文本 |
|---|---|
| \rm(roman) | \text |
A B,AB
\text{A B},\rm{A B}
A B,AB

AB,ABAB
\text A B,\rm A B\\
{\rm A} B
AB,ABAB
\rm 对其后所有字符都起作用
分式与根式

12,121x+y1x+1y+11x+1y+1
\frac{1}{2},\frac 1 2\\
\frac 1 {x+y}\\
\frac {\frac 1 x+1} {y+1} \\
\frac {\dfrac 1 x+1} {y+1}
21,21x+y1y+1x1+1y+1x1+1
调整分式的显示比例大小:\dfrac (display-style)

2,x+y,x3
\sqrt 2,\sqrt{x+y},\sqrt[3]x
2,x+y,3x
普通运算符
- \ge (greater than or equal ,大于等于)
- \le (less than or equal,小于等于)
- \equiv (equivalent,恒等于)
- \approx(approximate,约等于)
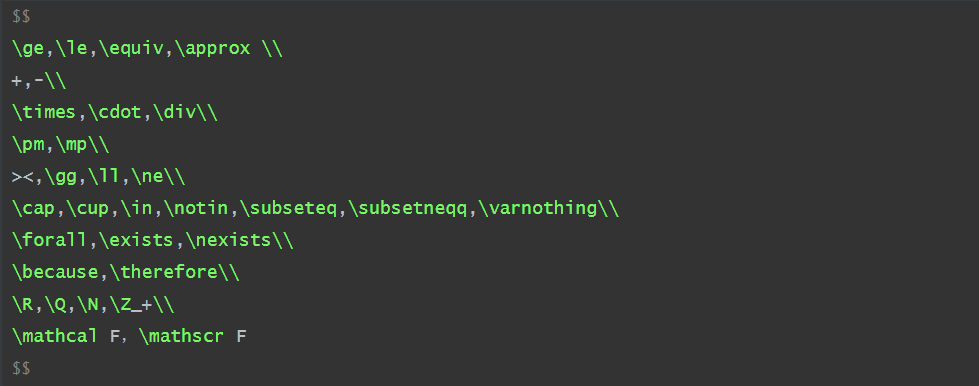
$$
\ge,\le,\equiv,\approx \
+,-\
\times,\cdot,\div\
\pm,\mp\
<,\gg,\ll,\ne\
\cap,\cup,\in,\notin,\subseteq,\subsetneqq,\varnothing\
\forall,\exists,\nexists\
\because,\therefore\
\R,\Q,\N,\Z_+\
\mathcal F,\mathscr F
$$
\mathscr(script,手写字体)
大型运算符

⋯ ,⋮,…,⋱
\cdots,\vdots,\dots,\ddots
⋯,⋮,…,⋱
\vdots(vertical,垂直的)
\ddots(diagonal,对角的)

∞,∂,∇,∝,°
\infty,\partial,\nabla,\propto,°
∞,∂,∇,∝,°
\propto (proportional to,正比于)

sinx,secx,cosxlog2x,lnx,lgxmaxx,MSE(x):直立体MSE:不正确
\sin x,\sec x,\cos x\\
\log_2 x,\ln x,\lg x\\
\max x,\text{MSE}(x):直立体\\
MSE:不正确
sinx,secx,cosxlog2x,lnx,lgxmaxx,MSE(x):直立体MSE:不正确

limx→0xsinx
\lim\limits_{x \to 0}\frac x {\sin x}
x→0limsinxx
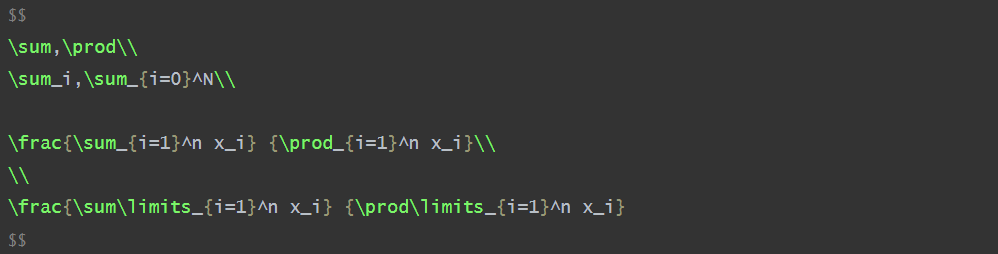
∑,∏∑i,∑i=0N
\sum,\prod\\
\sum_i,\sum_{i=0}^N\\
∑,∏i∑,i=0∑N
∑i=1nxi∏i=1nxi
\frac{\sum_{i=1}^n x_i} {\prod_{i=1}^n x_i}\\
∏i=1nxi∑i=1nxi
∑i=1nxi∏i=1nxi
\frac{\sum\limits_{i=1}^n x_i} {\prod\limits_{i=1}^n x_i}
i=1∏nxii=1∑nxi
\limits : 将参数从求和符号右侧转移到上下侧

∫∬,∭,∮,∯∫−∞0f(x)dx:错误写法,d前应该有空格∫−∞0f(x) dx:正确写法
\int \\
\iint,\iiint,\oint,\oiint\\
\int_{-\infty}^0 f(x) \text d x :错误写法,\text d前应该有空格\\
\int_{-\infty}^0 f(x) \, \text d x :正确写法
∫∬,∭,∮,∬∫−∞0f(x)dx:错误写法,d前应该有空格∫−∞0f(x)dx:正确写法
标注

x⃗,AB→xˉ,A‾a^,a˙
\vec x,\overrightarrow {AB}\\
\bar x,\overline{A}\\
\hat a,\dot a
x,ABxˉ,Aa^,a˙

箭头

←,⇐↑,↓,↕↗,↙,↖,↘
\leftarrow,\Leftarrow\\
\uparrow,\downarrow,\updownarrow\\
\nearrow,\swarrow,\nwarrow,\searrow
←,⇐↑,↓,↕↗,↙,↖,↘

括号

[()],{,}⌈,⌉,⌊,⌋(0,1a]∂x∂y∣x=0
[()],\{,\}\\
\lceil,\rceil,\lfloor,\rfloor\\
\left(0,\frac 1 a\right]\\
\left. \frac{\partial x}{\partial y} \right |_{x=0}
[()],{,}⌈,⌉,⌊,⌋(0,a1]∂y∂xx=0
\left ( : 高度自适应
\left . : 左侧虚拟匹配
多行公式

a=b+c+b=2b+b
\begin{align}
a=b+c+b\\
=2b+b
\end{align}
a=b+c+b=2b+b
默认是右对齐

a=b+c+b=2b+c
\begin{align}
a&=b+c+b\\
&=2b+c
\end{align}
a=b+c+b=2b+c
& 处进行匹配,最后再等号处对齐

f(x)={sinx,−π≤x≤π0,其他
f(x)=
\begin{cases}
\sin x,&-\pi\le x \le \pi \\
0,&\text{其他}
\end{cases}
f(x)={sinx,0,−π≤x≤π其他
矩阵

ab⋯c⋮⋮⋱⋮ef⋯g
\begin{matrix}
a & b & \cdots & c \\
\vdots &\vdots &\ddots & \vdots \\
e & f & \cdots &g
\end{matrix}
a⋮eb⋮f⋯⋱⋯c⋮g
无外括号
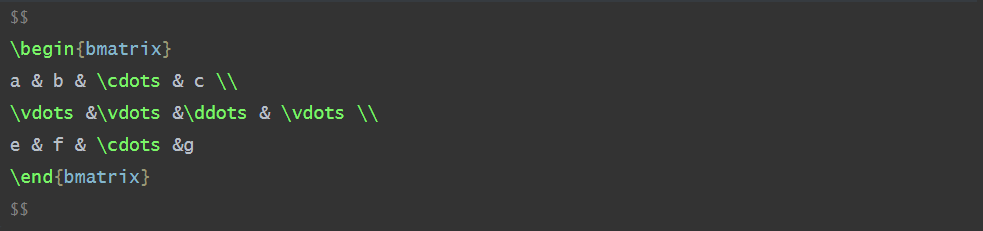
[ab⋯c⋮⋮⋱⋮ef⋯g]
\begin{bmatrix}
a & b & \cdots & c \\
\vdots &\vdots &\ddots & \vdots \\
e & f & \cdots &g
\end{bmatrix}
a⋮eb⋮f⋯⋱⋯c⋮g
bmartix ( bracket, 方括号)

(ab⋯c⋮⋮⋱⋮ef⋯g)
\begin{pmatrix}
a & b & \cdots & c \\
\vdots &\vdots &\ddots & \vdots \\
e & f & \cdots &g
\end{pmatrix}
a⋮eb⋮f⋯⋱⋯c⋮g
pmatrix (parenthesis,圆括号)

∣ab⋯c⋮⋮⋱⋮ef⋯g∣
\begin{vmatrix}
a & b & \cdots & c \\
\vdots &\vdots &\ddots & \vdots \\
e & f & \cdots &g
\end{vmatrix}
a⋮eb⋮f⋯⋱⋯c⋮g
vmatrix (vertical bar,竖向短线)

ABT
\bf A\\
\bf B^{\rm T}
ABT
\bf (blod face,粗体)
实战
f(x)=12πσe−(x−μ)22σ2
f(x)=\frac 1 {\sqrt {2\pi}\sigma} \text{e}^{-\frac{(x-\mu)^2}{2\sigma^2}}
f(x)=2πσ1e−2σ2(x−μ)2

f(x)=12πσe[−(x−μ)22σ2]
f(x)=\frac 1 {\sqrt {2\pi} \sigma}\text{e}\left [ -\frac{(x-\mu)^2}{2\sigma^2}\right]
f(x)=2πσ1e[−2σ2(x−μ)2]

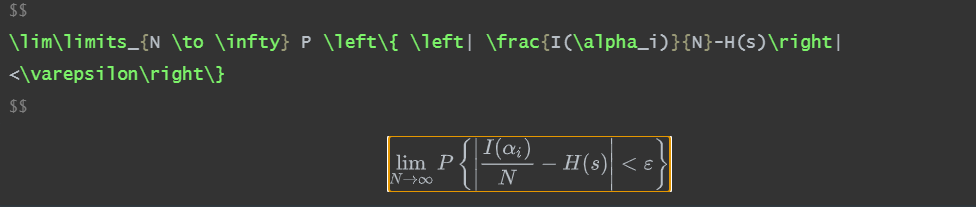
limN→∞P{∣I(αi)N−H(s)∣<ε}
\lim\limits_{N \to \infty} P \left\{ \left| \frac{I(\alpha_i)}{N}-H(s)\right|<\varepsilon\right\}
N→∞limP{NI(αi)−H(s)<ε}
x(n)=12π∫−ππX(ejω)ejωn dω
x(n)=\frac 1 {2\pi} \int_{-\pi}^{\pi} X(e^{\text{j}\omega})e^{\text{j}\omega n}\,\text{d}\omega
x(n)=2π1∫−ππX(ejω)ejωndω

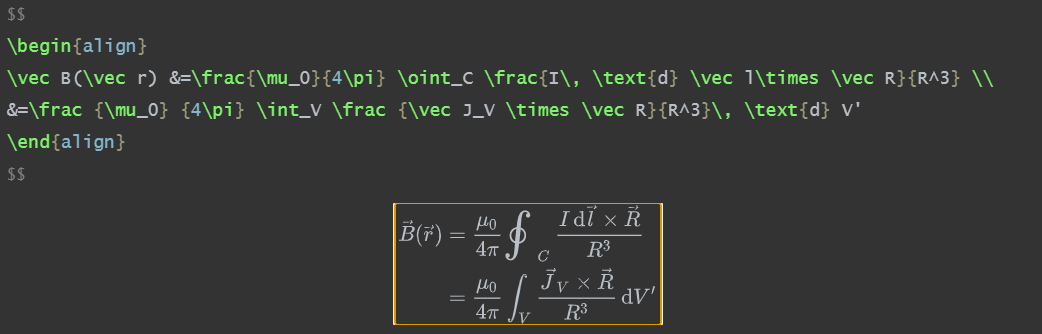
B⃗(r⃗)=μ04π∮CI dl⃗×R⃗R3=μ04π∫VJ⃗V×R⃗R3 dV′
\begin{align}
\vec B(\vec r) &=\frac{\mu_0}{4\pi} \oint_C \frac{I\, \text{d} \vec l\times \vec R}{R^3} \\
&=\frac {\mu_0} {4\pi} \int_V \frac {\vec J_V \times \vec R}{R^3}\, \text{d} V'
\end{align}
B(r)=4πμ0∮CR3Idl×R=4πμ0∫VR3JV×RdV′







 本文详细介绍了Markdown语言中常用的文本格式化标记,包括下划线、加粗、斜体、标题层次、列表、链接、图片、引用、表格、数学公式、代码块、LaTeX符号以及电磁学相关的数学表达式。
本文详细介绍了Markdown语言中常用的文本格式化标记,包括下划线、加粗、斜体、标题层次、列表、链接、图片、引用、表格、数学公式、代码块、LaTeX符号以及电磁学相关的数学表达式。

















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








