机器学习之正则化

正则化

概念

        正则化就是对最小化经验误差函数上加约束，约束有引导作用，使在优化误差函数的时候倾向于选择满足约束的梯度减少的方向，使最终的解倾向于符合先验知识。（来自百度百科，不理解没关系，可继续向后阅读）

为什么需要正则化

        在机器学习数据拟合过程中，会出现三种结果：
  
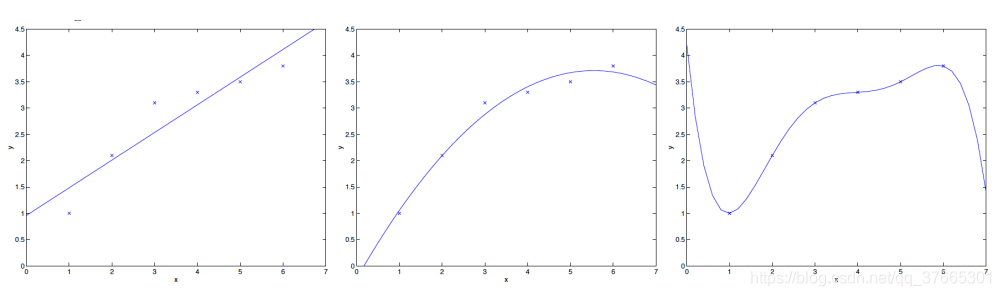
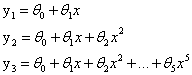
        y₁情况称为欠拟合，拟合程度不够，从训练数据中训练出的函数模型与实际数据偏差过大，无法正确表达出数据所具有的特征。
        y₂是我们期望的误差小的且可应用的拟合曲线
        y₃情况称为过拟合，函数模型过于符合训练数据，使其不能用于实际预测。
        对于过拟合我们可知若有m个训练数据，那么我们始终可以构造一个m-1次的方程，使其通过所有训练数据点。如果我们能解决过拟合问题，使我们训练出的方程能泛化到新的数据样本中，那么我们就获得了一个合适的预测函数。
        解决过拟合通常有两种方法：
        1. 减少特征变量的数量
        需要减少那些不需要的特征变量，去掉那些没用且会对拟合结果造成错误的特征变量。但我们在减少特征变量前需要先判断其是否不需要，一般而言，所有特征都会对结果造成影响，我们舍弃了一些信息，就会舍弃这些影响。需要保证舍弃的特征对所有的数据（训练数据和新数据）预测产生的影响都是极小的。
        2.正则化
        保留所有的特征变量，但是减小特征变量的数量级（通过减小变量前的参数）。当实验数据有很多无关紧要的特征时，正则化可以很好的发挥作用。

正则化思想

        一般我们通过不断地使代价函数减小来求解我们想要得到的特征变量前的参数θ，假设有函数y = θ₀+θ₁x+θ₂x²+θ₃x³+θ₄x⁴，我们想要x³和x⁴对我们的预测结果产生较小的影响，我们可以通过减小θ₃和θ₄来实现，如何减小θ₃和θ₄？可以通过添加惩罚项来实现。
        一般的代价函数：
        
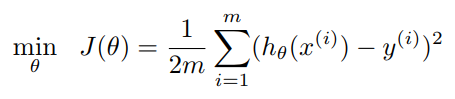
        添加了惩罚项的代价函数：
        
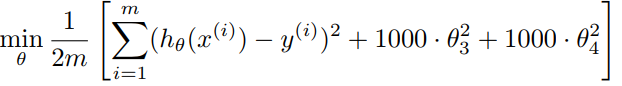
        1000 只是随便写的某个较大的数字而已。添加了惩罚项后，如果我们想要最小化这个函数，那么为了最小化这个新的代价函数，我们要让θ₃和θ₄尽可能小。θ₃和θ₄变小了，那么θ₃x³和θ₄x⁴就在函数中变得很小，对我们的预测产生的影响也就变得很小了。
        更一般的添加了惩罚项的代价函数：