Rethinking Minimal Sufficient Representation in Contrastive Learning 论文解读和感想

最新推荐文章于 2025-08-11 19:56:42 发布

原创最新推荐文章于 2025-08-11 19:56:42 发布 · 713 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #人工智能 #深度学习

本文深入探讨了对比学习在提取特征时存在的问题，即仅学习共享信息可能导致下游任务性能下降。作者提出了两个解决方案：特征重构输入和高维互信息估计，以保留更多任务相关信息。实验表明，这两种方法都能有效提升表征的质量，特别是在类别多且样本量少的任务中，重构方法表现更优。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

作为2022 CVPR 的oral，本文对contrastive learning提取的特征用于下游任务的不足进行了深入的思考，并提出了直观的解决方法，是一篇值得深度的好文。

我们知道对比学习通过无监督的方式训练提取输入数据的表征，方便下游任务，这种无监督的方式通常是通过学习某些增强不变性特征进行的，这里作者对学习的表征进行了两个定义：
1、充分表征，即包含所有增强样本的共享表征的表征。
2、最小充分表征，充分表征中最小的表征，即包含且仅包含所有增强样本的共享表征的表征。
（这里先粗略的给出两个定义的描述，后面将会通过公式的方式来详细的讲述。）
对比学习通过最大化不同增强样本的互信息进行训练，因此其学习目标是样本的充分表征，而由于训练时不同增强样本是相互监督的，因此其学习目标也就等价于获得不同增强样本的最小充分表征。
我们知道不同增强样本所包含的信息是不同的（否则对比学习就成为了一个恒等映射），因此不同增强样本所适应的下游任务也是有差别的，但是如果学习的表征只包含共享信息，而丢弃了不共享的任务相关信息（学习最小充分表征），势必会造成提取的表征对某些下游任务性能下降。
为了解决以上问题，显然就要对学习的表征引入更多的样本不共享的任务相关信息。然而这就遇到了一个阻碍，即我们进行对比学习时是无法访问下游任务的，因此我们无法直接通过下游任务来引入额外任务相关信息，为此作者提出了一种近似的解决方法：我们只要增大表征和输入的互信息，就可以间接的使表征保留更多任务相关信息。为此作者提出了两种实施方法：
1、通过特征重构输入
2、进行高维互信息估计
实验表明这两种方法都能达到效果。

接下来我们通过具体的公式来进行问题分析。假设 $v 1$ 和 $v 2$ 是输入数据的两个增强， $v 1$ 和 $v 2$ 是两个增强对应的表征，则对比学习的优化目标为：
在这里插入图片描述
$f_1()$ 和 $f_2()$ 是表征映射，在某些模型如SimCLR中，这两个映射是一样的。接下来我们通过公式对充分表征进行定义：

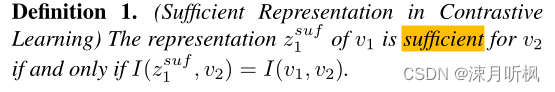
可以看到一个某个增强的特征是依赖其他增强的，样本 $v 1$ 对于样本 $v 2$ 的充分表征 $z 1$ 所包含的 $v 2$ 的信息和样本 $v 1$ 所包含的样本 $v 2$ 的信息是相同的。
接下来是最小充分标准：
在这里插入图片描述
可以看成是充分表征所包含信息的下界。
由于数据的表征所含的信息小于等于数据本身，因此我们有一下不等式：

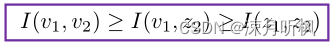
由于 $v 1$ 和 $v 2$ 是两个随机增强，因此其信息量可以看成是固定的，因此由公式(1)可知其优化的上界近似于 $I (z 1, z 1) = I (v 1, v 2)$ ，也就是充分表征。而由于在训练时一个样本的监督信息完全来自于另一个样本，因此公式(1)的优化目标就近似于最小充分表征。
由于下游任务各式各样，因此其需要的信息也不尽相同，我们用 $T$ 来表示下游任务需要的信息，那么当我们仅去获得不同样本的最小充分表征就会造成一个问题，假如 $v 1$ 包含大部分 $T$ 的信息，而 $v 2$ 只包含少部分，那么获得的表征就会忽视掉 $I (v 1, T ∣ v 2)$ ，这对于任务 $T$ 是非常不利的，具体的我们可以通过以下定理来表示：
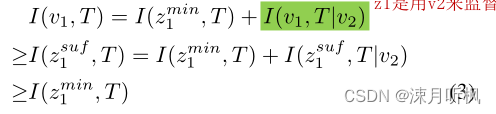
在这里插入图片描述

通过最左边列来看，对于任务 $T$ ，显然最小化充分表征是最差的，因为它完全忽视了绿色项的信息。通过信息图来看：
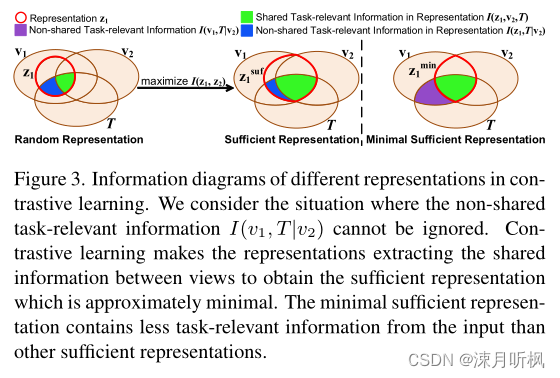
在这里插入图片描述
绿色部分是最小充分表征在任务 $T$ 中的有效信息，蓝色+绿色是充分表征在任务 $T$ 中的有效信息，紫色+绿色是样本 $v 1$ 在任务 $T$ 中的有效信息，因此接下来我们要想办法将紫色部分的信息给添加进去，至少是部分添加进去。
通过公式(3)，显然最直接的方式就是直接添加 $I (z 1, T ∣ v 2)$ ，然而很可惜，在训练时我们是无法访问 $T$ 的，因此作者通过一种替代的方案，即最小化表征和输入的互信息，即
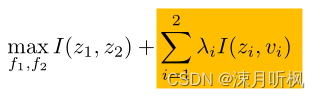
在这里插入图片描述
第一项不值得说，第二项作者通过以下两种具体实施方法：
首先第一种方法是希望通过表征来重建输入。这是很直观的， $z$ 和 $v$ 的互信息可以表示为 $I (z, v) = H (z) - H (v ∣ z)$ ，对于第一项我们是没法更改的，因此我们能做的就是最小化第二项条件能量，为此作者首先将其转化为了熵的形式：
在这里插入图片描述
这就是一个典型的自编码的解码问题。在实现的过程中作者为了使问题更便于求解，又采用了VAE的变分形式，将 $p (v ∣ z)$ 变分为某个更简单的分布 $q (v ∣ z)$ 。对于一个给定的方差 $σ\sigma$ ，用网络拟合其均值 $μ(z)\mu(z)$ ，然后采样，获得重构数据。因此通过这种方式的最终优化目标为：
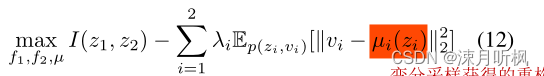
在这里插入图片描述
可以看到以上方法虽然可以解决我们的问题，但是需要引入很多额外的训练参数和计算量，并且对于许多复杂的输入数据是难以优化的，为此作者又提出了另一种方法，即通过互信息下界评估的方式。这里作者选用了InfoNCE的评估方式，但同时作者也在补充材料中指出，其他下界评估方式同样可用。对于输入的 $z$ 和 $v$ ，InfoNCE的具体形式如下：
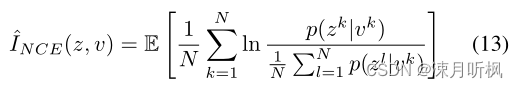
在这里插入图片描述
那么在具体实施时，上式的 $p (z ∣ v)$ 我们依然要用网络拟合，并且也用到了变分技巧。但是需要注意的是，相比于1是对输入进行重构，我们这里是对高纬特征进行重构，因此这里的重构网络可以要比1的简单，而且可以避免输入数据的复杂度对优化的影响：
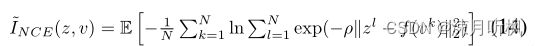
在这里插入图片描述
通过这个方法进行优化，我们最终高的优化目标为：

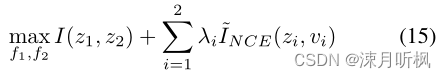
实验部分，我们只有一个点需要注意：
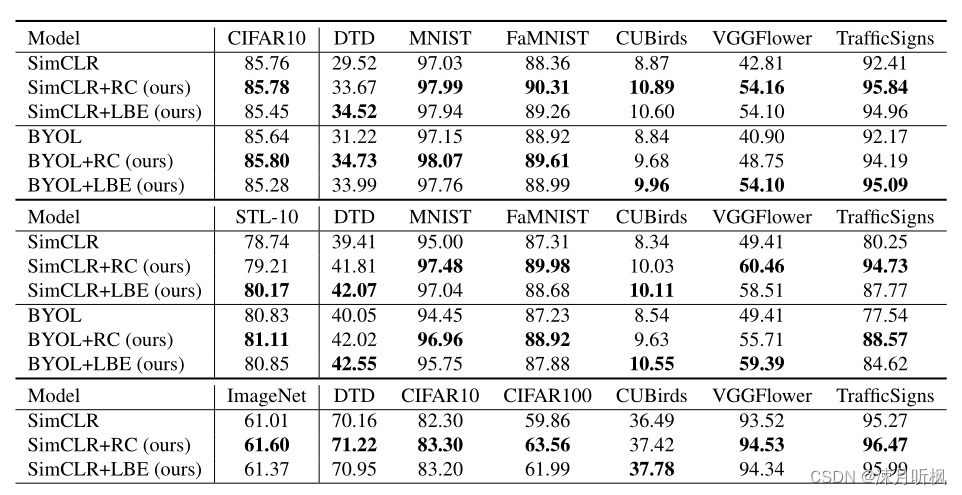
在这里插入图片描述

可以看到两种优化方法虽然都能达到一定的目的，但是相比较来说InfoNCE的效果要略差于样本重构。比较cifar10和cifar100可以看出，类别多并且每一类样本数据量少时，重构的效果要更好，但是其中CUB数据集比较另类，这个数据集中每类的差异性并不大，但是一共有200个类，因此进行样本重构的话是很难优化的（不同的特征重构出来的东西都差不多），所以相比较来说InfoNCE的高维特征比较优势就体现出来了。