目录
写在前面的唠叨:
最近这段时间一直在研究深度学习之类的东西,虽然如今对几种常见的神经网络都有了很好的了解,用起来也比较顺手,但是越学也越觉得瓶颈越来越明显了,最大的问题觉得还是数学基础不行,学习那些常见的模型已经把线性代数的知识捡的差不多了,而到了想自己设计模型的时候,才忽然发现微积分也是十分重要的,而这两年我都还给老师了呀T_T。所以把PRML这本书又翻了出来,推导一下里面的公式。
然而刚看到高斯分布里面的方差推导就抽了我一嘴巴,去网上查了查发现这部分推导大家写的都挺乱的,于是自己总结了一下,留作记录,省的以后在看的时候到处乱查,重新推……
归一化推导证明:
证明归一化,即证明:
首先我们将其展开:
这里将 替换掉有:
这里假设:
这个积分直接计算比较困难,但是可以绕个弯,采用极坐标的方式计算,首先我们将其求其平方:
在将其转化为极坐标,令可得:
即:
恩!大功告成!
期望(一阶矩)推导证明:
证明期望就比较简单了~
将 替换掉有:
这里为奇函数,所以该项积分为0,所以:
二阶矩推导证明:
就是这个东西,推了一上午都没推出来,最后还是的问了周围考研的同学,真是耻辱,被挂起来抽。这里给出了两种推导方式:
1. 展开利用Gamma函数进行求解:
将 替换掉有:
这里令第一项中,即有:
这里用到了函数,也就是我们通常说的伽马函数,它的定义是这样的:
这里有几个特殊值,感兴趣的话可以记一下。
特殊值内容来自中文wiki,所以出错了不负责哦,嘿嘿……
当然这里用到了伽马函数,也可以采用不用伽马函数的方法。
2. 直接积分求解:
啊~这个就是我同学的方法,实名感谢猛某,如果多年后您看见这篇博客别忘了朝我要稿费。
方差推导证明:
既然我们已经求的了一阶矩、二阶矩,那么再求方差就简单了:
当然方差也可以直接求,因为这部分已经有前辈推导过了,我就直接上图了!(才不是嫌麻烦,不想写latex代码)
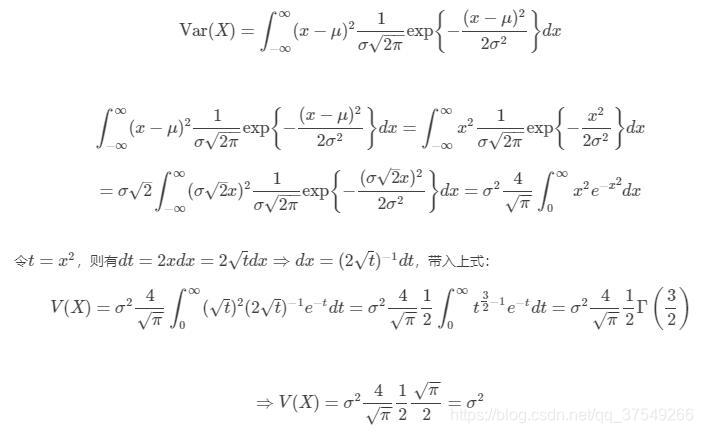
这里标明出处,前辈的推导很棒,给了我很大帮助。
留个坑:
本来是想写个PRML的全公式推导的读书笔记,然而码完了这些代码,突然觉得好麻烦收获好大,尽力吧,如果时间充裕会补一补,留个坑,溜……






 这篇博客详细介绍了高斯分布的归一化、期望和方差的推导过程。作者在研究深度学习时意识到微积分的重要性,并尝试自己推导高斯分布的数学性质。归一化通过极坐标转换得以证明,期望的求解相对直接,而二阶矩的推导涉及Gamma函数。方差的计算则利用一阶矩和二阶矩。博客最后提到,作者计划完成更全面的公式推导笔记。
这篇博客详细介绍了高斯分布的归一化、期望和方差的推导过程。作者在研究深度学习时意识到微积分的重要性,并尝试自己推导高斯分布的数学性质。归一化通过极坐标转换得以证明,期望的求解相对直接,而二阶矩的推导涉及Gamma函数。方差的计算则利用一阶矩和二阶矩。博客最后提到,作者计划完成更全面的公式推导笔记。
















 1923
1923

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








