排序算法研究之归并排序（Merge sort）

前面几个小节，我们分别介绍了冒泡排序，插入排序，直接快速排序 ，选择排序 ， 希尔排序， 堆排序本节，我们介绍基于归并操作的归并排序。

１、算法思想

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用，归并排序将两个已经有序的序列合并成一个有序的序列。

2、算法流程

主要两步(分，合)
步骤１进行序列拆分，这是一递归的操作，通常是分到只剩一个元素。（一个元素必定是有序的）
步骤２对排好序的序列合并。
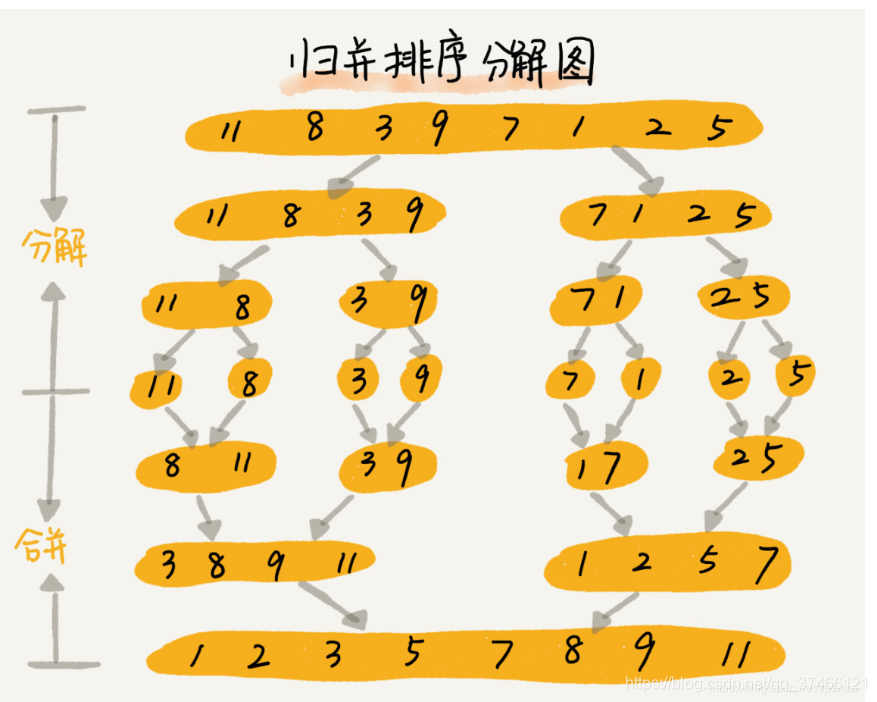
思路：假设我们有一个没有排好序的序列，那么我们首先使用分割的方法将这个序列分割成一个个已经排好序的子序列（直到剩下一个元素）。然后再利用归并的方法将一个个有序的子序列合并成排好序的序列。

具体流程可见下图，截取自博主　zpznba　感谢分享！！

3、算法优缺点

优点：
高效，稳定，和选择排序一样不受输入数据影响，但是要比选择排序好的多最坏时间复杂度 = 平均时间复杂度 O(nlogn)
缺点：
需要辅助空间来构建临时数组。

４、主要代码ｃ++

例子：输入一个有10个元素的数组，并对其进行归并排序，最后数组为升序

/***************************************************************************
 *  @file       Merge_sort.cpp
 *  @author     Shawn
 *  @date       26  March 2019
 *  @remark     26  March 2019
 *  @theme      Merge Sort
 ***************************************************************************/
# include<iostream>
using namespace std;

void Merge(int [], int, int, int, int []);
// 归并排序划分过程
void MergeSort(int a[], int left, int right, int temp[])
{
    if(left < right)
    {
        int mid = (left + right) >> 1;
        MergeSort(a,left,mid,temp);
        MergeSort(a,mid+1,right,temp);
        Merge(a,left,mid,right,temp);
    }
}

// 归并排序合并过程
// 将数组下标范围[left,mid]和[mid+1,right]的有序序列合并成一个有序序列
void Merge(int a[], int left, int mid, int right, int temp[])
{
    int p0 = 0;
    int p1 = left, p2 = mid + 1;
    // p0指向辅助数组的首位
    // p1指向数组[left,mid]的首位,p2指向数组[mid+1,right]的首位
    // 开始排序，< 先放小元素升序，>降序
    while(p1<=mid && p2<=right)
    {
        if(a[p1] < a[p2])
            temp[p0++] = a[p1++];
        else
            temp[p0++] = a[p2++];
    }
    ////如果还有剩余元素，直接放入到辅助数组中
    while(p1<=mid)
        temp[p0++] = a[p1++];
    while(p2<=right)
        temp[p0++] = a[p2++];
    // 拷贝temp排好顺序的元素到数组a中，
    // 注意数组a是从left开始的，不能默认为0，并且一共有元素right-left+1个元素。
    for(int i=0; i<right-left+1;++i)
        a[left+i] = temp[i];
}
int main()
{
    int array [] = {55,2,6,4,32,12,9,73,26,37};
    int len = sizeof(array) / sizeof(int);
    cout<<"输入的原始序列:  ";
    for(int i=0; i<len; i++) // 输出原序列
        cout<<array[i]<<",";
    cout<<endl<<endl;

    cout<<"  ----堆排序结果---- " << endl;
    int *temp = new int [len];
    MergeSort(array,0,len-1,temp); // 调用排序函数
    for(int j=0; j<len; j++)
        cout<<array[j]<<",";

    return 0;
}