平衡二叉树

定义

它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

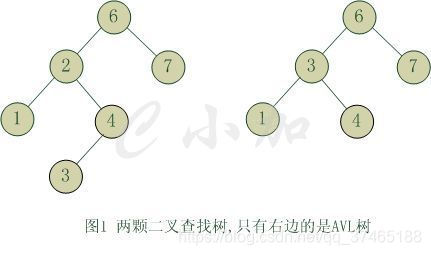
平衡因子(bf)：结点的左子树的深度减去右子树的深度，那么显然-1<=bf<=1,这里我们定义:

#define EH 0；
#define LH 1；
#define RH -1；//依次为等高，左高，右高。
typedef struct _BitNode
{
    int data;
    int bf;//平衡因子
    struct _BitNode *lchild,*rchild;
}BitNode,*BiTree;

平衡二叉树大部分操作和二叉查找树类似，主要不同在于插入删除的时候平衡二叉树的平衡可能被改变，并且只有从那些插入点到根结点的路径上的结点的平衡性可能被改变，因为只有这些结点的子树可能变化。

旋转:

前面说过，如果在AVL树中进行插入或删除节点后，可能导致AVL树失去平衡。这种失去平衡的可以概括为4种姿态：LL(左左)，LR(左右)，RR(右右)和RL(右左)。下面给出它们的示意图：

上图中的4棵树都是"失去平衡的AVL树"，从左往右的情况依次是：LL、LR、RL、RR。除了上面的情况之外，还有其它的失去平衡的AVL
上面的两张图都是为了便于理解，而列举的关于"失去平衡的AVL树"的例子。总的来说，AVL树失去平衡时的情况一定是LL、LR、RL、RR这4种之一。

(1) LL：LeftLeft，也称为"左左"。插入或删除一个节点后，根节点的左子树的左子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。
例如，在上面LL情况中，由于"根节点(8)的左子树(4)的左子树(2)还有非空子节点"，而"根节点(8)的右子树(12)没有子节点"；导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。

(2) LR：LeftRight，也称为"左右"。插入或删除一个节点后，根节点的左子树的右子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。
例如，在上面LR情况中，由于"根节点(8)的左子树(4)的左子树(6)还有非空子节点"，而"根节点(8)的右子树(12)没有子节点"；导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。

(3) RL：RightLeft，称为"右左"。插入或删除一个节点后，根节点的右子树的左子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。
例如，在上面RL情况中，由于"根节点(8)的右子树(12)的左子树(10)还有非空子节点"，而"根节点(8)的左子树(4)没有子节点"；导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。

(4) RR：RightRight，称为"右右"。插入或删除一个节点后，根节点的右子树的右子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。

LL旋转:

LL失去平衡的情况，可以通过一次旋转让AVL树恢复平衡。如下图：

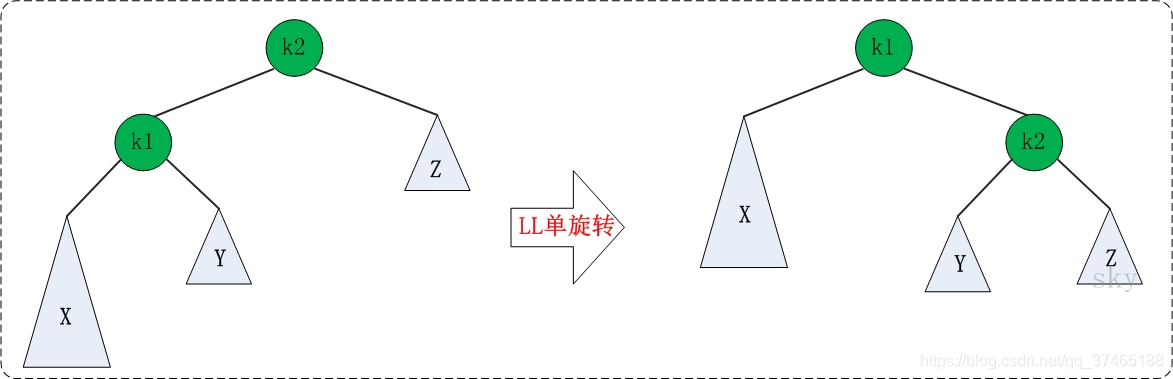
代码:

 * LL：左左对应的情况(左单旋转)。
 *
 * 返回值：旋转后的根节点
 */
static Node* left_left_rotation(AVLTree k2)
{
    AVLTree k1;

    k1 = k2->left;
    k2->left = k1->right;
    k1->right = k2;

    k2->height = MAX( HEIGHT(k2->left), HEIGHT(k2->right)) + 1;
    k1->height = MAX( HEIGHT(k1->left), k2->height) + 1;

    return k1;
}

RR旋转:

理解了LL之后，RR就相当容易理解了。RR是与LL对称的情况！RR恢复平衡的旋转方法如下：

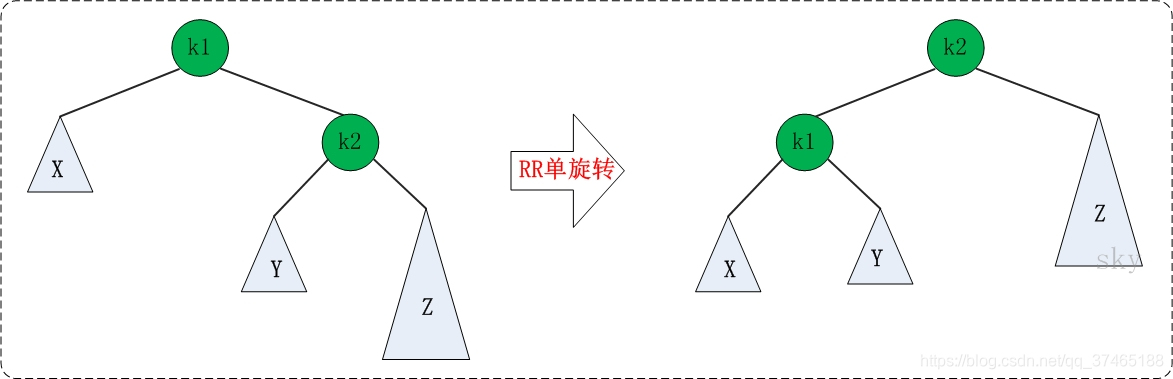
代码:

/*
 * RR：右右对应的情况(右单旋转)。
 *
 * 返回值：旋转后的根节点
 */
static Node* right_right_rotation(AVLTree k1)
{
    AVLTree k2;

    k2 = k1->right;
    k1->right = k2->left;
    k2->left = k1;

    k1->height = MAX( HEIGHT(k1->left), HEIGHT(k1->right)) + 1;
    k2->height = MAX( HEIGHT(k2->right), k1->height) + 1;

    return k2;
}

LR的旋转

代码:

/*
 * LR：左右对应的情况(左双旋转)。
 *
 * 返回值：旋转后的根节点
 */
static Node* left_right_rotation(AVLTree k3)
{
    k3->left = right_right_rotation(k3->left);

    return left_left_rotation(k3);
}

RL的旋转：

代码:

/*
 * RL：右左对应的情况(右双旋转)。
 *
 * 返回值：旋转后的根节点
 */
static Node* right_left_rotation(AVLTree k1)
{
    k1->right = left_left_rotation(k1->right);

    return right_right_rotation(k1);
}

插入:

/* 
 * 将结点插入到AVL树中，并返回根节点
 *
 * 参数说明：
 *     tree AVL树的根结点
 *     key 插入的结点的键值
 * 返回值：
 *     根节点
 */
Node* avltree_insert(AVLTree tree, Type key)
{
    if (tree == NULL) 
    {
        // 新建节点
        tree = avltree_create_node(key, NULL, NULL);
        if (tree==NULL)
        {
            printf("ERROR: create avltree node failed!\n");
            return NULL;
        }
    }
    else if (key < tree->key) // 应该将key插入到"tree的左子树"的情况
    {
        tree->left = avltree_insert(tree->left, key);
        // 插入节点后，若AVL树失去平衡，则进行相应的调节。
        if (HEIGHT(tree->left) - HEIGHT(tree->right) == 2)
        {
            if (key < tree->left->key)
                tree = left_left_rotation(tree);
            else
                tree = left_right_rotation(tree);
        }
    }
    else if (key > tree->key) // 应该将key插入到"tree的右子树"的情况
    {
        tree->right = avltree_insert(tree->right, key);
        // 插入节点后，若AVL树失去平衡，则进行相应的调节。
        if (HEIGHT(tree->right) - HEIGHT(tree->left) == 2)
        {
            if (key > tree->right->key)
                tree = right_right_rotation(tree);
            else
                tree = right_left_rotation(tree);
        }
    }
    else //key == tree->key)
    {
        printf("添加失败：不允许添加相同的节点！\n");
    }

    tree->height = MAX( HEIGHT(tree->left), HEIGHT(tree->right)) + 1;

    return tree;
}

删除:

/* 
 * 删除结点(z)，返回根节点
 *
 * 参数说明：
 *     ptree AVL树的根结点
 *     z 待删除的结点
 * 返回值：
 *     根节点
 */
static Node* delete_node(AVLTree tree, Node *z)
{
    // 根为空 或者 没有要删除的节点，直接返回NULL。
    if (tree==NULL || z==NULL)
        return NULL;

    if (z->key < tree->key)        // 待删除的节点在"tree的左子树"中
    {
        tree->left = delete_node(tree->left, z);
        // 删除节点后，若AVL树失去平衡，则进行相应的调节。
        if (HEIGHT(tree->right) - HEIGHT(tree->left) == 2)
        {
            Node *r =  tree->right;
            if (HEIGHT(r->left) > HEIGHT(r->right))
                tree = right_left_rotation(tree);
            else
                tree = right_right_rotation(tree);
        }
    }
    else if (z->key > tree->key)// 待删除的节点在"tree的右子树"中
    {
        tree->right = delete_node(tree->right, z);
        // 删除节点后，若AVL树失去平衡，则进行相应的调节。
        if (HEIGHT(tree->left) - HEIGHT(tree->right) == 2)
        {
            Node *l =  tree->left;
            if (HEIGHT(l->right) > HEIGHT(l->left))
                tree = left_right_rotation(tree);
            else
                tree = left_left_rotation(tree);
        }
    }
    else    // tree是对应要删除的节点。
    {
        // tree的左右孩子都非空
        if ((tree->left) && (tree->right))
        {
            if (HEIGHT(tree->left) > HEIGHT(tree->right))
            {
                // 如果tree的左子树比右子树高；
                // 则(01)找出tree的左子树中的最大节点
                //   (02)将该最大节点的值赋值给tree。
                //   (03)删除该最大节点。
                // 这类似于用"tree的左子树中最大节点"做"tree"的替身；
                // 采用这种方式的好处是：删除"tree的左子树中最大节点"之后，AVL树仍然是平衡的。
                Node *max = avltree_maximum(tree->left);
                tree->key = max->key;
                tree->left = delete_node(tree->left, max);
            }
            else
            {
                // 如果tree的左子树不比右子树高(即它们相等，或右子树比左子树高1)
                // 则(01)找出tree的右子树中的最小节点
                //   (02)将该最小节点的值赋值给tree。
                //   (03)删除该最小节点。
                // 这类似于用"tree的右子树中最小节点"做"tree"的替身；
                // 采用这种方式的好处是：删除"tree的右子树中最小节点"之后，AVL树仍然是平衡的。
                Node *min = avltree_maximum(tree->right);
                tree->key = min->key;
                tree->right = delete_node(tree->right, min);
            }
        }
        else
        {
            Node *tmp = tree;
            tree = tree->left ? tree->left : tree->right;
            free(tmp);
        }
    }

    return tree;
}

/* 
 * 删除结点(key是节点值)，返回根节点
 *
 * 参数说明：
 *     tree AVL树的根结点
 *     key 待删除的结点的键值
 * 返回值：
 *     根节点
 */
Node* avltree_delete(AVLTree tree, Type key)
{
    Node *z; 

    if ((z = avltree_search(tree, key)) != NULL)
        tree = delete_node(tree, z);
    return tree;
}