HDU 6134 Battlestation Operational (莫比乌斯反演+积性函数筛)*

Battlestation Operational

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 752    Accepted Submission(s): 420

 

Problem Description

> The Death Star, known officially as the DS-1 Orbital Battle Station, also known as the Death Star I, the First Death Star, Project Stardust internally, and simply the Ultimate Weapon in early development stages, was a moon-sized, deep-space mobile battle station constructed by the Galactic Empire. Designed to fire a single planet-destroying superlaser powered by massive kyber crystals, it was the pet project of the Emperor, Darth Vader, and its eventual commander Grand Moff Wilhuff Tarkin to expound the military philosophy of the aptly named Tarkin Doctrine.
>
> — Wookieepedia

In the story of the Rogue One, the rebels risked their lives stolen the construction plan of the Death Star before it can cause catastrophic damage to the rebel base. According to the documents, the main weapon of the Death Star, the Superlaser, emits asymmetric energy in the battlefield that cause photons to annihilate and burns everything in a single shot.

You are assigned the task to estimate the damage of one shot of the Superlaser.

Assuming that the battlefield is an n×n grid. The energy field ignited by the Superlaser is asymmetric over the grid. For the cell at i-th row and j-th column, ⌈i/j⌉ units of damage will be caused. Furthermore, due to the quantum effects, the energies in a cell cancel out if gcd(i,j)≠1 or i<j.

The figure below illustrates the damage caused to each cell for n=100. A cell in black indicates that this cell will not be damaged due to the quantum effects. Otherwise, different colors denote different units of damages.

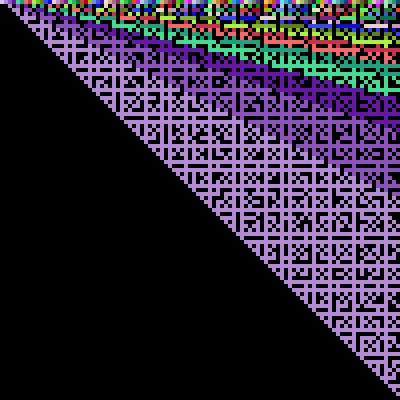
Your should calculate the total damage to the battlefield. Formally, you should compute

f(n)=∑i=1n∑j=1i⌈ij⌉[(i,j)=1],

where [(i,j)=1] evaluates to be 1 if gcd(i,j)=1, otherwise 0.

 

 

Input

There are multiple test cases.

Each line of the input, there is an integer n (1≤n≤106), as described in the problem.

There are up to 104 test cases.

 

 

Output

For each test case, output one integer in one line denoting the total damage of the Superlaser, f(n) mod 109+7.

 

 

Sample Input

1 2 3 10

 

 

Sample Output

1 3 8 110

 

 

Source

2017 Multi-University Training Contest - Team 8

 

 

Recommend

liuyiding   |   We have carefully selected several similar problems for you:  6447 6446 6445 6444 6443 

 

 

#pragma comment(linker, "/STACK:102400000,102400000")
#include<bits/stdc++.h>
using namespace std;

#define debug puts("YES");
#define rep(x,y,z) for(int (x)=(y);(x)<(z);(x)++)

#define lrt int l,int r,int rt
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define ll long long

const int  maxn =1e6+5;
const int mod=1e9+7;

ll gcd(ll x,ll y) { return y==0?x:gcd(y,x%y); }

///正因子个数函数（不是质因子）
int prim[maxn],cnt=0;
int miu[maxn],phi[maxn];
bool vis[maxn];

int g[maxn];
ll f[maxn],sum[maxn];
/*
题目大意：求公式

可以说是蛮难的一道莫比乌斯题目了，
参杂着一些常用的数论公式转换和套路。
首先函数明显是个前缀和的形式，
那么单独求一项f(i),
....具体的求法参考大佬的博客吧，我手打公式不会。
https://blog.youkuaiyun.com/consciousman/article/details/77888386

*/
void sieve()
{
    miu[1]=phi[1]=sum[1]=1;
    memset(vis,false,sizeof(vis));
    for(int i=2;i<maxn;i++)
    {
        if(!vis[i])
        {
            prim[cnt++]=i;miu[i]=-1;
            g[i]=1;///初始化
            phi[i]=i-1;sum[i]=2;
        }
        for(int j=0;j<cnt;j++)
        {
            int k=i*prim[j];
            if(k>=maxn) break;
            vis[k]=true;
            if(i%prim[j]==0)
            {
                g[k]=g[i]+1;sum[k]=sum[i]+sum[i]/g[k];
                phi[k]=phi[i]*prim[j];
                break;///注意这里的莫比乌斯函数是零
            }
            g[k]=1;sum[k]=sum[i]<<1;
            miu[k]=-miu[i];phi[k]=phi[i]*(prim[j]-1);
        }
    }

    for(int i=2;i<maxn;i++) sum[i]+=sum[i-1];
    for(int i=1;i<maxn;i++)
        for(int j=i,k=1;j<maxn;j+=i,k++)
        {
            (f[j]+=miu[k]*sum[i])%=mod;
            if(f[j]<0) f[j]=(f[j]+mod)%mod;
        }
    for(int i=1;i<maxn;i++) f[i]=(f[i]+phi[i]-1+f[i-1])%mod;
}

int main()
{
    sieve();
    int n;
    while(scanf("%d",&n)!=EOF) printf("%lld\n",f[n]);
    return 0;
}