PAT甲级-2021秋-第4题-笛卡尔树-AC代码

7-4 Sorted Cartesian Tree (30 分)

A Sorted Cartesian tree is a tree of (key, priority) pairs. The tree is heap-ordered according to the priority values, and an inorder traversal gives the keys in sorted order. For example, given the pairs { (55, 8), (58, 15), (62, 3), (73, 4), (85, 1), (88, 5), (90, 12), (95, 10), (96, 18), (98, 6) }, the increasing min-heap Cartesian tree is shown by the figure.

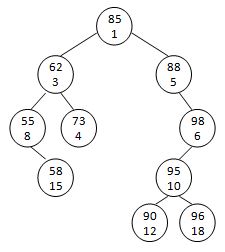
Your job is to do level-order traversals on an increasing min-heap Cartesian tree.

Input Specification:

Each input file contains one test case. Each case starts from giving a positive integer N (≤30), and then N lines follow, each gives a pair in the format key priority. All the numbers are in the range of int.

Output Specification:

For each test case, print in the first line the level-order traversal key sequence and then in the next line the level-order traversal priority sequence of the min-heap Cartesian tree.

All the numbers in a line must be separated by exactly one space, and there must be no extra space at the beginning or the end of the line.

Sample Input:

10
88 5
58 15
95 10
62 3
55 8
98 6
85 1
90 12
96 18
73 4

Sample Output:

85 62 88 55 73 98 58 95 90 96
1 3 5 8 4 6 15 10 12 18

满分题解

/**
 * 题目：PAT_A实战-BST-中等-2021秋-笛卡尔树
 *
 * 说明：
 * 1. 输入：整数n, 与n个(key,priority)二元组
 * 2. 任务：如上所述
 * 3. 输出：层序遍历的笛卡尔树的key, 层序遍历的笛卡尔树的priority
 *
 * 技巧：
 * 1. 笛卡尔树其实是一个独有概念，做题时还不知道，在想是当成特殊的BST还是特殊的堆
 *    分析后感觉更像特殊的BST
 * 2. 插入建树的算法：
 *    a. 把节点序列按照prio排序
 *    b. 把排序后的节点依次按照插入BST的常规方法插入BST, 只不过比较的是key
 *
 */
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<map>
#include<queue>
using namespace std;

#define MAXN        109

typedef struct p_t
{
    int key;
    int prio;
    p_t(int k, int p) :key(k), prio(p) {}
    bool operator<(const p_t& x)const
    {
        if (prio != x.prio) {
            return prio < x.prio;
        }
        else {
            return key < x.key;
        }
    }
}p_t;

typedef struct node_t {
    int id;
    struct node_t* lc, * rc;
}node_t;

int n;
vector<p_t> pairs;
node_t* root;

void ins_bst(node_t*& r, int idn)
{
    if (r == NULL) {
        r = new node_t;
        r->id = idn;
        r->lc = r->rc = NULL;
    }
    else if (pairs[idn].key < pairs[r->id].key) {
        ins_bst(r->lc, idn);
    }
    else {
        ins_bst(r->rc, idn);
    }
}

void bfs(node_t* u, bool isk)
{
    int cnt = 0;

    node_t* x = u;
    queue<node_t*> q;
    q.push(x);
    while (!q.empty()) {
        x = q.front();
        q.pop();

        printf("%d", (isk == true) ? pairs[x->id].key : pairs[x->id].prio);
        if (cnt < n - 1) {
            cout << " ";
        }
        ++cnt;

        if (x->lc != NULL) {
            q.push(x->lc);
        }
        if (x->rc != NULL) {
            q.push(x->rc);
        }
    }
}

int main(void)
{
    cin >> n;
    for (int i = 0; i < n; ++i) {
        int k_in, p_in;
        cin >> k_in >> p_in;
        pairs.push_back(p_t(k_in, p_in));
    }
    sort(pairs.begin(), pairs.end());

    root = NULL;
    for (int i = 0; i < (int)pairs.size(); ++i) {
        ins_bst(root, i);
    }

    bfs(root, true);
    cout << endl;
    bfs(root, false);

    return 0;
}