从零开始学数据结构与算法-线性结构-栈、队列

栈

栈只允许访问一个数据项，即最后插入的数据项。移除这个数据项才能访问倒数第二个插入的数据项。（后进先出）

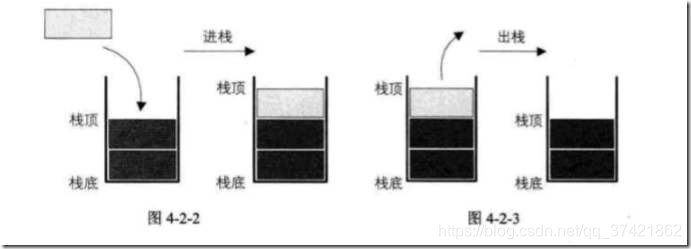
数组实现栈

// 通过数组实现栈
public class StackX {
	private int maxSize;
	private long[] stackArray;
	private int top;

	public StackX(int size) {
		maxSize = size;
		stackArray = new long[maxSize];
		top = -1;
	}

	public void push(long value) {
		stackArray[++top] = value;
	}

	public long pop() {
		return stackArray[top--];
	}

	public long peek() {
		return stackArray[top];
	}

	public boolean isEmpty() {
		return top == -1;
	}

	public boolean isFull() {
		return top == maxSize - 1;
	}
}

入栈和出栈操作时间复杂度均为 O(1)。

栈操作所耗时间不依赖栈中数据项的个数，操作时间短，因为不需要进行比较和移动操作。

队列

在队列中第一个插入的数据项会被最先移除（先进先出），相比于栈是相反的。

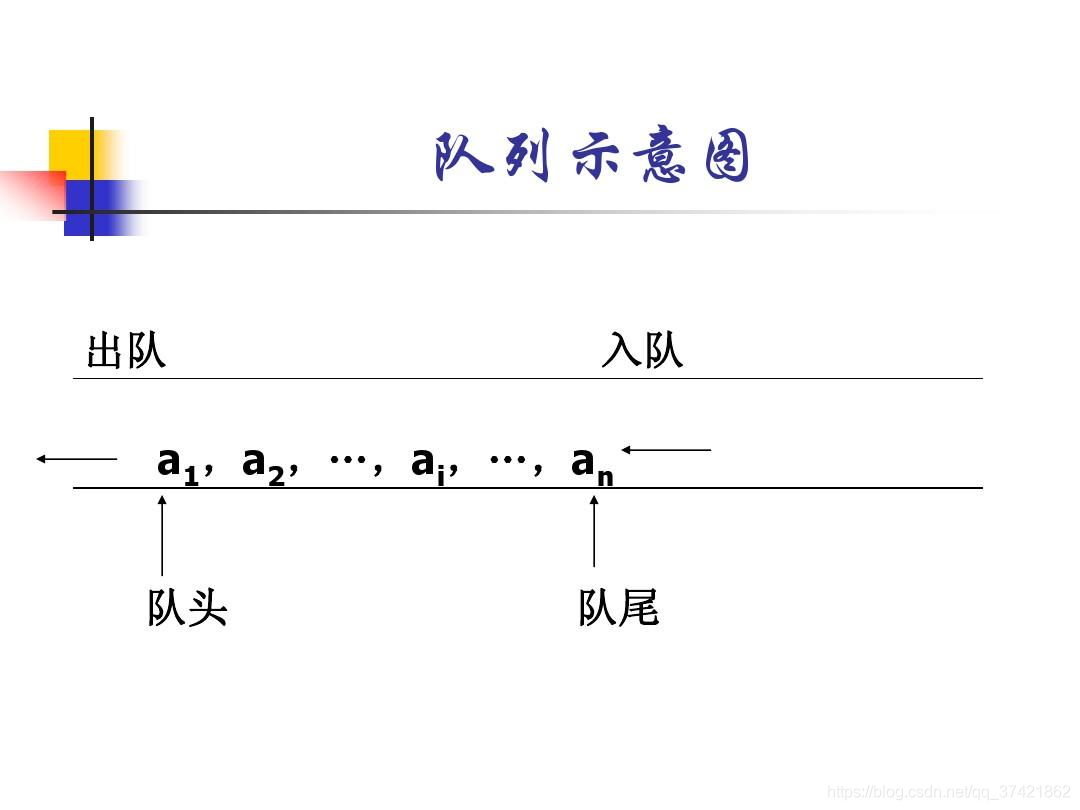
数组实现队列

public class Queue {
	private int maxSize;
	private long[] queArray;
	private int front; // 队头
	private int rear; // 队尾
	private int nItems;

	public Queue(int maxSize) {
		this.maxSize = maxSize;
		this.queArray = new long[this.maxSize];
		this.front = 0;
		this.rear = -1;
		this.nItems = 0;
	}

	public void insert(long value) {
		if (rear == maxSize - 1)
			rear = -1;
		queArray[++rear] = value;
		nItems++;
	}

	public long remove() {
		long temp = queArray[front];
		queArray[front++] = 0;
		if (front == maxSize)
			front = 0;
		nItems--;
		return temp;
	}

	public long peekFront() {
		return queArray[front];
	}

	public boolean isEmpty() {
		return nItems == 0;
	}

	public boolean isFull() {
		return nItems == maxSize;
	}

	public int size() {
		return nItems;
	}
}

和栈一样，队列中插入数据项和移除数据项的时间复杂度均为 O(1) 。

优先级队列

优先级队列是比栈和队列更专用的数据结构，像普通队列一样，优先级队列有一个队头和队尾，并且也是在队头移除数据项。在优先级队列中，数据项按关键字的值有序，这样关键字最小（或者最大）的数据项总在队头，数据项在插入时按照顺序插入到合适的位置以确保队列的顺序。

public class PriorityQueue {
	private int maxSize;
	private long[] queArray;
	private int nItems;

	public PriorityQueue(int maxSize) {
		this.maxSize = maxSize;
		this.queArray = new long[this.maxSize];
		this.nItems = 0;
	}

	public void insert(long value) {
		int j;
		if (nItems == 0) {
			this.queArray[nItems++] = value;
		} else {
			for (j = nItems - 1; j >= 0; j--) {
				if (value > this.queArray[j]) {
					this.queArray[j + 1] = this.queArray[j];
				} else {
					break;
				}
			}
			this.queArray[j + 1] = value;
			this.nItems++;
		}
	}

	public long remove() {
		long temp = this.queArray[--nItems];
		this.queArray[nItems] = 0;
		return temp;
	}

	public long peekMin() {
		return this.queArray[nItems - 1];
	}

	public boolean isEmpty() {
		return this.nItems == 0;
	}

	public boolean isFull() {
		return this.nItems == this.maxSize;
	}

	public void print() {
		for (long temp : this.queArray) {
			System.out.print(temp + " ");
		}
		System.out.println();
	}
	
	public static void main(String[] args) {
		PriorityQueue priorityQueue = new PriorityQueue(5);
		
		priorityQueue.insert(20);
		priorityQueue.insert(10);
		priorityQueue.insert(50);
		priorityQueue.insert(30);
		priorityQueue.insert(40);
		priorityQueue.print();
		priorityQueue.remove();
		priorityQueue.remove();
		priorityQueue.remove();
		priorityQueue.insert(30);
		priorityQueue.insert(60);
		priorityQueue.insert(70);
		priorityQueue.print();
	}
}

数组实现的优先级队列，插入操作需要 O(N) 的时间，删除操作需要 O(1) 的时间。

扩展

算法题-用两个栈实现队列

用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

import java.util.Stack;

public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();
    
 	public void push(int node) {

		stack1.push(node);
	}

	public int pop() {

		if (!stack2.isEmpty()) {
			return stack2.pop();
		} else {
			while (!stack1.isEmpty()) {
				stack2.push(stack1.pop());
			}
		}
		return stack2.isEmpty() ? -1 : stack2.pop();
	}
}

算法题-包含min函数的栈

定义栈的数据结构，请在该类型中实现一个能够得到栈中所含最小元素的min函数（时间复杂度应为O（1））

import java.util.Stack;

public class Solution {
	private Stack<Integer> stack = new Stack<Integer>();
	private int[] minArray = new int[9999];// 用于存放递增的元素
	private int effectiveLength = 0;// 数组中有效元素所占有的长度

	public void push(int node) {
        // 第一个元素直接放到minArray的最左边
		if (stack.isEmpty()) {
			minArray[0] = node;
		} else {
            // 如果新加入的元素比数组中最小的小，
            // 将node放到下标0位置，数组中其他元素后移
			if (node < minArray[0]) {
				for (int i = effectiveLength - 1; i > -1; i--) {
					minArray[i + 1] = minArray[i];
				}
				minArray[0] = node;
			} else {
                // 找到node的位置，将之后的元素后移
				for (int i = 0, len = effectiveLength; i < len; i++) {
					int temp = minArray[i];
					if (node < temp) {
						for (int j = len - 1; j >= i; j--) {
							minArray[j + 1] = minArray[j];
						}
						minArray[i] = node;
						break;
					}
                    // node为最大的元素，放到数组最后面
					if (i + 1 == len) {
						minArray[i + 1] = node;
					}
				}
			}
		}
        // 有效长度+1
		effectiveLength++;
		stack.push(node);
	}

	public void pop() {
		if (!stack.isEmpty()) {
			Integer popTemp = stack.pop();
			for (int i = 0, len = effectiveLength; i < len; i++) {
				int minTemp = minArray[i];
                // 找到相同值元素，将其从数组中移出
				if (minTemp == popTemp) {
					for (int j = i; j < effectiveLength; j++) {
						minArray[j] = minArray[j + 1];
					}
				}
			}
            // 有效长度-1
            effectiveLength--;
		}
	}

	public int top() {

		return stack.peek();
	}

	public int min() {
        // 直接返回数组中最左边的元素，即栈中最小元素
		return minArray[0];
	}
}