[C++ & BP神经网络] 傻陈带你用C++实现BP

最新推荐文章于 2025-06-14 13:27:19 发布

IcyLeaves

最新推荐文章于 2025-06-14 13:27:19 发布

阅读量3k

点赞数 6

CC 4.0 BY-SA版权

分类专栏： AI Learning

本文链接：https://blog.youkuaiyun.com/qq_37398834/article/details/84189148

AI Learning 专栏收录该内容

3 篇文章

订阅专栏

本文深入讲解BP神经网络的原理和C++实现，包括输入层、隐含层、输出层的计算，权重和偏置的调整，以及误差反向传播算法。通过实例演示，帮助读者理解神经网络的工作机制。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

人工智能的算法需要许多预备知识，但时间比较紧，所以我只会对"对最后算法实现有帮助的资料"感兴趣，试着在不完全了解的情况下将这次实验完成。
环境的配置请参考我的另一个实验[C++ & AdaBoost] 傻陈带你用C++实现AdaBoost，关于数据集的C++载入，这里也不再赘述了。

BP神经网络

BP神经网络原理及C++代码实现
 BP神经网络计算过程详解，用笔手算一遍弄懂反向传播
 用BP神经网络解决简单的分类问题
 神经网络的偏置值是什么意思
 BP神经网络算法学习—处理流程（伪代码）
BP神经网络算法学习—基础理论1
BP神经网络同样有着很多各式各样的教程，这里摘取了几篇对我帮助极大的博客。

介绍

BP神经网络鲜明的特点自然是他的神经网络，不过再继续深入就会遇到繁琐的数学运算和一堆专业术语，因此我要先大致介绍一下。
1.输入层、隐含层、输出层
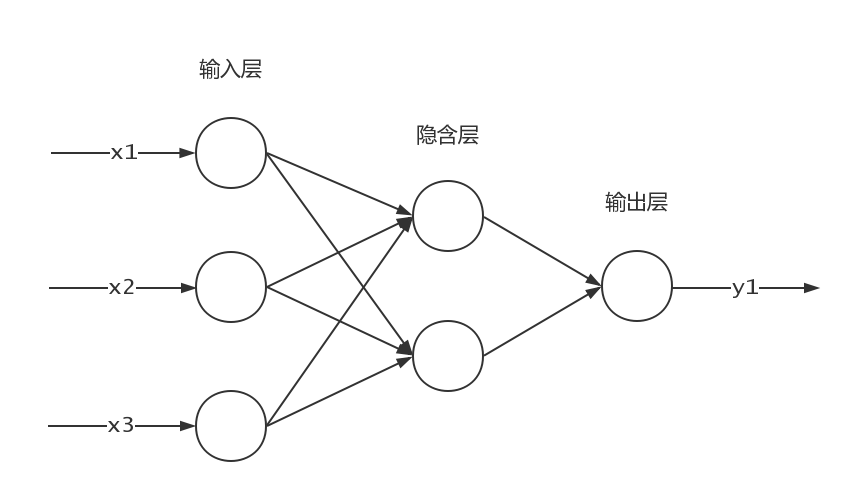在这里插入图片描述神经网络有三大层，两层之间都是全连接关系，连接的边上都会赋予权重。
输入层：一般来说，输入有多少维度，输入层就有多少节点。例如本实验的数据集一组记录有64个输入的属性，所以输入层需要64个节点
隐含层：隐含层需要多少个节点也没有确切的说法。但可以从少数个逐渐增加，观察预测的性能，最后确定一个最佳值。本次实验我就直接暂定了。
输出层：因为我们最后只要分两类——0或1，因此可以在输出层设置2个节点，理想的分类结果是，类0的输出节点值是[0,1]，类1的输出节点值是[1,0]。
2.权重
在层与层之间的每根连线上，都会带上权重。输入从左向右传递时，数据经过权重边就必须要乘上权重才能前进，连线汇聚到一个节点就把这些连线的值都相加。权重的初始值一般可以是(-1,1)的随机数。
3.偏置（阈值)
在隐含层和输出层的每个节点上，都会带上偏置。将上一层的结果接收相加后，最后还要加一个偏置来做出适当调整。
4.激活函数
上面得到的还不是最后的值，我们要给这个值使用一个归一化函数来限定值的范围，一般常用的是Sigmoid函数。
5.误差
输出层的结果会与预期理想结果产生误差，BP算法可以反向传播这个误差来调整权重和偏置。我们的目标就是把最后的误差收敛到我们想要的范围内。
6.学习率
反向传播时的一个自定义参数，[0,1]之间，学习率越小，学的越仔细，但学习速度也越慢。

思路

输入-输出
- 初始化：64个节点的输入层，6个（暂定）节点的隐含层，2个节点的输出层，随机64×6+6×2个权重值，随机6+2个偏置值，取类1和类0的记录各100条。
- 向输入层输入一条记录的64个属性。一个节点放一个值。
- 隐含层的节点接收输入层的输入，并作出偏置，使用激活函数得到最终的节点值。
- 输出层的节点接收隐含层的输入，并作出偏置，使用激活函数得到最终的输出结果。
- 调入记录的类别，计算误差。
输出-输入
- 利用输出层的结果和误差，来调整整个网络所有的权值和偏置。

公式

神经网络的难点就在于其令人头大的公式，因此从头到尾梳理一遍是非常重要的。这里就直接给出最后的结果了，推导过程就参考上面的引用资料吧。

变量说明

数据集的样本可以看作一个64维的输入向量和一个2维的输出向量：
$\mathbf{x}=\left \{ x_{1},x_{2},...,x_{63},x_{64} \right \}$ $\mathbf{t}=\left \{ t_{1},t_{2} \right \}$ 第L层第i个节点接收上层的数据后，总输入为
$Z_{i}^{L}$ 第L层第i个节点的输出为
$a_{i}^{L}$ 第L层第i个节点到第L+1层的第j个节点的连线权重为
$W_{i,j}^{L}$ 第L层第i个节点的偏置为
$b_{i}^{L-1}$

输入层的输入

输入层第i个节点的输入值：
$Z_{i}^{1}=x_{i}$ Example
输入层第35个节点的输入为
$Z_{35}^{1}=x_{35}$

输入层的输出

输入层第i个节点的输出直接等于输入：
$a_{i}^{1}=Z_{i}^{1}$ Example
输入层第35个节点的输出为
$a_{35}^{1}=Z_{35}^{1}$

隐含层的输入

隐含层第i个节点的输入值等于输入层输出的加权求和加上此隐含层节点的偏置：
$Z_{i}^{2}=\left (\sum_{j=1}^{64}W_{j,i}^{1}\cdot a_{j}^{1}\right )+b_{i}^{1}$ Example
隐含层第4个节点的输入值为
$Z_{4}^{2}=\left (\sum_{j=1}^{64}W_{j,4}^{1}\cdot a_{j}^{1}\right )+b_{4}^{1}$

激活函数Sigmoid

$f(x)=\frac{1}{1+e^{-x}}$

隐含层的输出

隐含层第i个节点的输出值等于该节点输入值的激活函数值：
$a_{i}^{2}=f\left ( Z_{i}^{2} \right )$ Example
隐含层第6个节点的输出值为
$a_{6}^{2}=f\left ( Z_{6}^{2} \right )$

输出层的输入

输出层第i个节点的输入值等于隐含层输出的加权求和加上此输出层节点的偏置：
$Z_{i}^{3}=\left (\sum_{j=1}^{6}W_{j,i}^{2}\cdot a_{j}^{2}\right )+b_{i}^{2}$ Example
输出层第2个节点的输入值为
$Z_{2}^{3}=\left (\sum_{j=1}^{6}W_{j,2}^{2}\cdot a_{j}^{2}\right )+b_{2}^{2}$

输出层的输出

输出层第i个节点的输出值等于该节点输入值的激活函数值：
$a_{i}^{3}=f\left ( Z_{i}^{3} \right )$ Example
输出层第2个节点的输出值为
$a_{2}^{3}=f\left ( Z_{2}^{3} \right )$

误差计算

在一条样本中，输出的误差为：
$E=\frac{1}{2}\sum_{j=1}^{2}\left ( t_{j}-a_{j}^{3} \right )^{2}$

隐含层→输出层权值调整

隐含层第i个节点到输出层第j个节点的连线权值变化为，学习率为η：
$W_{i,j}^{2}=W_{i,j}^{2}-\eta \left ( a_{j}^{3}-t_{j} \right )\left ( 1- a_{j}^{3}\right )a_{j}^{3}a_{i}^{2}$ Example
隐含层第2个节点到输出层第1个节点的连线权值变化为，学习率η为0.2
$W_{2,1}^{2}=W_{2,1}^{2}-0.2 \left ( a_{1}^{3}-t_{1} \right )\left ( 1- a_{1}^{3}\right )a_{1}^{3}a_{2}^{2}$

输出层偏置调整

输出层第j个节点的偏置变化为，学习率为η：
$b_{j}^{2}=b_{j}^{2}-\eta \left ( a_{j}^{3}-t_{j} \right )\left ( 1- a_{j}^{3}\right )a_{j}^{3}$ Example
输出层第1个节点的偏置变化为，学习率η为0.2
$b_{1}^{2}=b_{1}^{2}-\eta \left ( a_{1}^{3}-t_{1} \right )\left ( 1- a_{1}^{3}\right )a_{1}^{3}$

输入层→隐含层权值调整

输入层第i个节点到隐含层第j个节点的连线权值变化为，学习率为η：
$W_{i,j}^{1}=W_{i,j}^{1}-\eta a_{i}^{1}a_{j}^{2}\left ( 1-a_{j}^{2} \right )\sum_{k=1}^{2}\left ( a_{k}^{3}-t_{k} \right )\left ( 1- a_{k}^{3}\right )a_{k}^{3}W_{j,k}^{2}$ Example
输入层第42个节点到隐含层第5个节点的连线权值变化为，学习率η为0.2
$W_{42,5}^{1}=W_{42,5}^{1}-0.2 a_{42}^{1}a_{5}^{2}\left ( 1-a_{5}^{2} \right )\sum_{k=1}^{2}\left ( a_{k}^{3}-t_{k} \right )\left ( 1- a_{k}^{3}\right )a_{k}^{3}W_{5,k}^{2}$

隐含层偏置调整

隐含层第j个节点的偏置变化为，学习率为η：
$b_{j}^{1}=b_{j}^{1}-\eta a_{j}^{2}\left ( 1-a_{j}^{2} \right )\sum_{k=1}^{2}\left (a_{k}^{3} -t_{k}\right )\left ( 1- a_{k}^{3}\right )a_{k}^{3}W_{j,k}^{2}$ Example
隐含层第4个节点的偏置变化为，学习率η为0.2
$b_{4}^{1}=b_{4}^{1}-\eta a_{4}^{2}\left ( 1-a_{4}^{2} \right )\sum_{k=1}^{2}\left ( a_{k}^{3}-t_{k} \right )\left ( 1- a_{k}^{3}\right )a_{k}^{3}W_{4,k}^{2}$