Container With Most Water--MaxArea

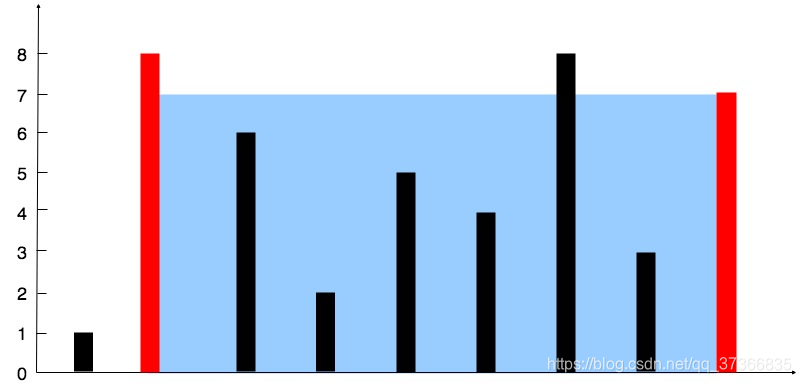
给定n个非负正整数{a1,a2,a3,…,an}， 每个整数表示一个坐标{i，ai}. 他们表示x轴上的垂直直线，起点为{i, 0}，终点为{i,ai}, 寻找两条直线，使得两条直线之间可容纳水最大。如图所示。

Example:

Input: [1,8,6,2,5,4,8,3,7]
Output: 49

分析：
方法1，双重遍历，计算每个点与其他所有点的最大容积，最后取最大值。时间复杂度O（n2）.空间O（1）
方法2，观察可得知，容积受到两个参数的影响，其一为两个垂直直线中较小的一个，其二为横坐标长度。因此，可以双向开始遍历，记录每次的值，保留最大值，每次取小的直线位移。时间复杂度O（n），空间O（1）。

public static int maxArea(int[] height) {
int maxarea = 0, l = 0, r = height.length - 1;
while (l < r) {
maxarea = Math.max(maxarea, Math.min(height[l], height[r]) * (r - l));
if (height[l] < height[r])
l++;
else
r–;
}
return maxarea;
}