神经网络快速入门

目录

从一道例题讲起

生物学的启发

感知机

模型的建立

机器学习的“学习”

权重的优化

进一步思考

---

神经网络是比较常见的算法，适用于分类和预测等问题。

本文讲解最简单的神经网络模型：感知机。

从一道例题讲起

例题：景区规定14周岁的儿童以下可买半价票。但儿童往往没有身份证，难以准确判断年龄，如何根据一个人的身高和体重，判断是否达到14周岁？

分析：一般的经验，就是测一下身高体重，根据主观经验断定。例如一个儿童身高1.2m、体重30kg，基本可以确定是14周岁以下。

但仅凭主观经验，难免引起争执。如果一个人身高2米、体重100kg，坚持说自己才8岁，那到底给不给他半价呢？

生物学的启发

针对“由身高和体重判断是否达到14周岁”这个问题，在现实中，我们是通过人脑的神经系统做出判断。

神经系统的基本单元就是一个神经元：

单个神经元的结构：

• 神经元的树突收到输入信号（人眼看到的光信号等）

• 信号刺激细胞核，达到一定的阈值后会产生输出

• 该输出就是进一步的信号，继续传到下一个神经元

如此信号传下去，达到人脑的中枢神经等等，最终做出判断。

根据神经元的启发，便有了最简单的神经网络模型：感知机。

感知机就是仿照单个神经元，根据输入信号是否达到阈值，得到“输出”还是“不输出”的结果。

进一步地，如果我们多个神经元相连接，构成一整个系统，那就是传统的神经网络了。所以，感知机模型是神经网络的基础。今天先从感知机讲起，后续会详细讲解BP神经网络等模型。

感知机

感知机的结构很简单，只有输入层和输出层两大部分。

工作过程：

• 输入层：输入身高𝑥1和体重数据𝑥2

• 激活函数：综合判断输入信号是否达到阈值

• 输出层：激活函数就在输出层，求得的函数值就是输出值𝑦

怎么用感知机求解问题呢？

模型的建立

题目要求根据身高和体重，判断此人是否达到了14周岁。

我们把题目“翻译”成数学语言：

1、题目类型是根据输入的数据，做出“是”和“否”的判断，符合感知机模型；

2、需要“综合考虑”身高和体重，数学上可以用加权线性求和实现。“加权”代表着不同变量的重要性，“求和”意味着所有的变量都考虑进去了；

3、判断“是否达到14周岁”，可以用加权线性求和与阈值b的差值作为判断标准，即作为激活函数的自变量。

4、求解结果只能有“未达到”和“达到”两种情况，可分别用0和1代表；

5、因此感知机中激活函数的函数值只能有0和1，符合此要求的函数叫做阶跃函数；

根据以上5步，建立感知机模型：

注意：阈值b可看作输入值固定为“-1”的节点所对应的权重，实现权重与阈值的统一，方便运算。图中的运算方法求得的t，与线性求和后再减去阈值b的结果完全一样。

图中，变量t就是“综合考虑所有因素并与阈值比较”的结果，也就是线性求和与阈值的差值。

显然，该差值t越大，意味着“综合考虑”的结果和阈值相差的大，也就更容易做出判断。

例如已知一个人身高10光年、体重100吨，那么很容易判断出此人不会是14周岁以下。

此时的感知机输出值为1，则判定此人达到了14周岁。问题也就解决了。

机器学习的“学习”

整个模型如下图：x是已知的身高和体重数据；f是激活函数，本题采用阶跃函数；y为待求的输出值；

显然该模型还需要确定权重w！

此时问题转化为：3个权重𝑤该怎么设定？

一般在模型初试化时， 查相关文献或主观经验设定权重。

但这样做主观性太大，求得的结果可能不理想，到底该如何科学地设定权重？

此时就需要让模型去“学习”：从已知的数据中学得模型。

学习的本质，就是不断地更改权重𝑤，使得模型求出的预测值尽可能地接近真实值。

例如，我们挨家挨户调查户口，搜集了十万人的身高、体重和年龄数据。

比赛中所需要的大量数据该如何找？

【数学建模 | 快速入门】数模基础+MATLAB入门+论文写作+模型算法精讲(小白数模国赛必看)https://www.bilibili.com/video/BV1Rq4y1S7S8?p=6我们先主观设定模型中的权重（例如都设成1），把这十万人的身高和体重代入感知机模型，求得十万个预测值。

别忘了，我们调查的时候，是已知了十万人的年龄，也就已知十万个“是否达到14周岁”的真实值。

把每一个人的预测值和真实值相比较，如果预测值都等于真实值，说明该模型完美。

如果预测值和真实值相差很大，那么就需要更改权重，使得两者的差值减小一些。

学习过程：

1. 模型初始化，人为主观地设置权重𝑤（查文献、靠经验）
2. 搜集大量的身高 、体重和是否达到14周岁的数据，称为训练数据集
3. 将搜集到的身高和体重代入模型，求得估计值
4. 将估计值与实际值(搜集到的“是否大于14周岁”)比较，差别越小越好
5. 若未满足终止条件，则继续对权重进行优化，得到新的权重，再重复步骤3，直到满足终止条件。

终止条件：估计值和实际值的差别小到一定程度为止。

学习过程结束后，模型就能较为准确地根据身高和体重判断一个人是否达到14周岁了。整个模型也就可以用了。

但学习过程的第5步所说的“优化”，具体该怎么做？

权重的优化

感知机的优化方法：

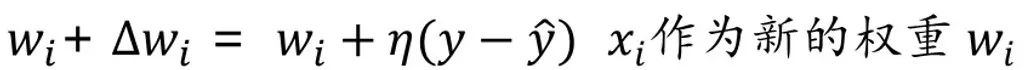
其中，𝜂∈(0,1)，称为学习率，𝜂过大容易震荡，过小则收敛速度太慢，通常设为0.1。

式中两个y(预测值和真实值)已知，学习率人为设定，那么就能得到新的权重了，也就实现了优化。

当达到终止条件时，此时的𝑤就作为模型的权重，模型就彻底建好了。

以后再有游客来，上秤、测身高，代入模型，求得预测值y，从而判断是否达到14周岁。

以后要是还有人身高2米、体重100kg，坚持说自己才8岁，那就：

注意：本文所讲的是感知机的优化方法，更复杂的神经网络还有其他的优化方法，例如梯度下降。以后讲到BP神经网络时会详细讲解。

进一步思考

学习过程中，终止条件是“估计值和实际值的差别小到一定程度为止”，但这个“差别”该如何衡量？“差别”又得是多小的才能终止？

激活函数除了本文所讲的阶跃函数，还有其他形式吗？分别有什么特点？适用于什么问题？

如果学习过程中始终达不到终止条件怎么办？

以上问题，会在后续的BP神经网络中讲解。