机器学习中的高斯过程

 

0.前言

写这篇文章的目的就是为了总结一下最近在学习的高斯过程的一些内容，但是由于我是初学者可能有些地方理解不到位，请大家多多谅解~文末附上了一些数学方面的推导。

1. 高斯过程定义

高斯过程是在连续域上定义的一种随机过程，可以看成连续域中所有随机变量的一组集合，并且任意单个或多个随机变量均满足一维高斯分布或者多维高斯分布。

一个高斯过程可以由一个均值函数以及一个协方差函数(也叫kernel function)确定，记为GP~（m(x), k(x, x')）。

2. 先验高斯过程

2.1 高斯过程的样本

假设我们在[0,1]区间定义一个均值函数为m(x) = 0，且采用,kernel = Standard Exponential(SE)(lengthscale=0.05,=1)的高斯过程。

当我们没有任何样本点的信息时，我们可以根据下面这个步骤得到一个先验高斯过程（Prior Gaussian Process）。

1.给定mean和covariance(kernel)function，比如我们使用的m(x)=0 & kernel = SE。

2.给定mean以及kernel中的hyperparameter的初始值，比如mean=0，就不用给出超参数；kernel =SE时, 需要给出其中的lengscale &  (后面会介绍这俩种超参数的意义)。

3. 给定想要产生的样本函数定义域，比如我们定义的范围[-1,1]，当然GP的样本是无限的，但是我们不可能取到无限个点，所以我们需要均匀取点，比如在给定的[-1,1]中取均匀的100个点。

4.有了kernel，有了hyperparameter的初始值，有个具体的样本函数的范围和点，那么我们就可以计算出对应的kernel的covariance matrix，记为C。

5.对C进行SVD分解，C = usv'

6.从标准正态分布中产生n个点的样本，记为

7.即为我们所求的高斯过程样本。

具体原因，请看下列这个定理：

足以说明，我们生成的就是一个高斯过程的样本。

执行上述步骤，我们得到5个GP的样本，如下图所示：

                                                                              5条高斯过程的样本

这个曲线好像并没有什么规律，当我们进行500次采样时

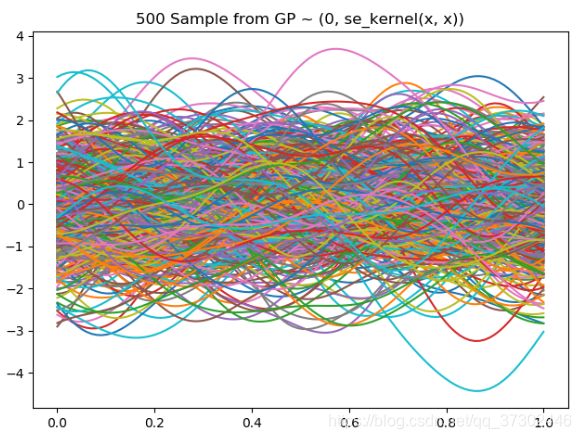
                                                                             500条高斯过程的样本

我们似乎可以看到这些曲线似乎围绕着0轴在上下波动，这里就体现了我们之前定义的m(x)的作用。

如果对x=0.5这个点进行采样的话，我们会得到下面这个直方图。