51nod1113 矩阵快速幂

最新推荐文章于 2019-09-01 22:58:49 发布

原创最新推荐文章于 2019-09-01 22:58:49 发布 · 355 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#矩阵快速幂

数论同时被 2 个专栏收录

15 篇文章

订阅专栏

题目集 - 51nod

9 篇文章

订阅专栏

本文深入讲解了矩阵快速幂的概念及其实现，通过对比传统的数的快速幂，详细介绍了矩阵快速幂的二进制拆分原理，并提供了完整的C++代码实现，包括矩阵乘法和矩阵快速幂的模板。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

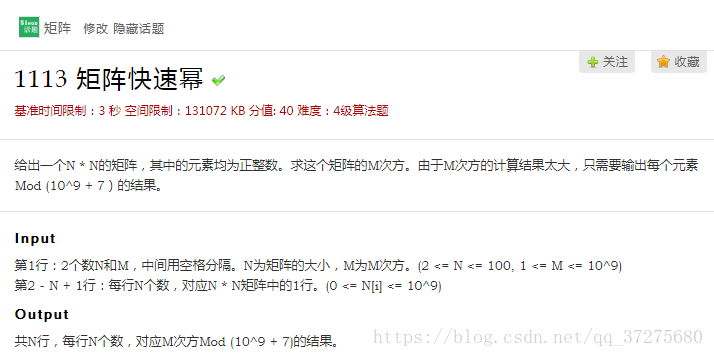
传送门：51nod1113 矩阵快速幂

Input示例
2 3
1 1
1 1
Output示例
4 4
4 4
矩阵乘法

今天开始学习矩阵快速幂，和之前学的数的快速幂没什么不同，只不过矩阵快速幂是以矩阵为单位的。

快速幂的原理都是二进制拆分，学习视频如下：SWPU-ACM每周算法讲堂-矩阵快速幂以及其他快速幂

相应的题目集：SWPU 2017暑假专题训练-矩阵快速幂

这个模板是视频中的大佬写的，直接拿来用了。

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn=110;
const int MOD=1e9+7;
#define mod(x) ((x)%MOD)

int n;

struct mat{
	int m[maxn][maxn];
}unit;

mat operator * (mat a,mat b){
	mat ret;
	ll x;
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++){
			x=0;
			for(int k=0;k<n;k++)
				x+=mod((ll)a.m[i][k]*b.m[k][j]);
			ret.m[i][j]=mod(x);
		}
		return ret;
}

void init_unit(){
	for(int i=0;i<maxn;i++)
		unit.m[i][i]=1;
	return ;
}

mat pow_mat(mat a,ll n){
	mat ret=unit;
	while(n){
		if(n&1) ret=ret*a;
		a=a*a;
		n>>=1;
	}
	return ret;
}


int main(){
	ll x;
	init_unit();
	while(~scanf("%lld%lld",&n,&x)){
		mat a;
		for(int i=0;i<n;i++)
			for(int j=0;j<n;j++)
				scanf("%d",&a.m[i][j]);
				
		a=pow_mat(a,x);
		for(int i=0;i<n;i++)
			for(int j=0;j<n;j++){
				if(j==n-1)
					printf("%d\n",a.m[i][j]);
				else 
					printf("%d ",a.m[i][j]);
			}
	}
	return 0;
}