聚类概念:
- 无监督问题:我们手里没有某一个数据属于某一个标签
- 聚类:将相似的东西分到一组
- 难点:不像有监督问题有标签 评估难度大 没有标准答案调参难

K-MEANS算法基本概念:
- 要得到簇的个数,需要制定K值
- 质心:数据的均值,即向量各维取平均即可
- 距离的度量:常用欧式距离和余弦相似度(先标准化)
- 优化目标:使得每个簇当中,所有样本点到质心的距离越小越好
m i n ∑ i = 1 k ∑ x ϵ C i d i c t ( C i , x ) 2 min\sum_{i=1}^k\sum_{x\epsilon C_i} dict(C_i,x)^2 mini=1∑kxϵCi∑dict(Ci,x)2
工作流程:
- 输入数据集
- 设置K值
- 初始化K个质心
- 遍历所有点,基于初始化的质心 算距离
- 使用现有数据更新质心
- 重新遍历所有样本点,基于更新后的质心算距离
- 选质心 更新质心

K-MEANS算法优缺点
- 优势
- 简单,快速,适合常规数据集
- 劣势
- K值难确定,普遍需要设置多组看效果
- 复杂度与样本呈线性关系
- 很难发现任意形状的簇
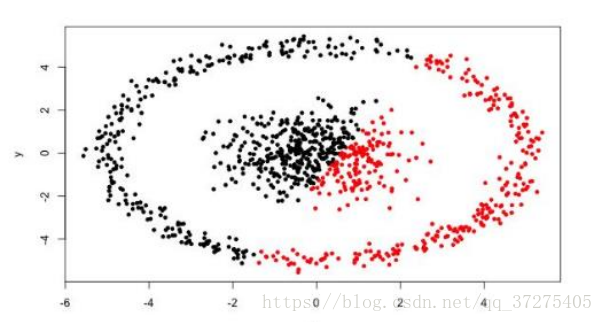
DBSCAN算法
基本概念:(Density-Based Spatial Clustering of Applications with Noise)
- 核心对象:若某个点的密度达到算法设定的阈值则为核心点(即r邻域内点的数量不小于minPts)
- e-邻域的距离阈值:设定的半径r
- 直接密度可达:若某点p在点q的r邻域内,且q是核心点则p-q直接密度可达
- 密度可达:若有一个点的序列q0、 q1、 …qk,对任意qi-qi-1是直接密度可达的 ,则称从q0到qk密度可达,这实际上是直接密度可达的“传播”。
- 密度相连:若从某核心点p出发,点q和点k都是密度可达的,则称点q和点k是密度相连的
- 边界点:属于某一个类的非核心点,不能发展下线了
- 噪声点:不属于任何一个类簇的点,从任何一个核心点出发都是密度不可达的
图解
- A:核心对象
- B,C:边界点
- N:离群点

工作流程
- 输入的参数
- 参数D:输入数据集
- 参数e:指定半径r
- MinPts:密度阈值
- DBSCAN算法迭代过程
- 将所有数据标记为没有被访问到
- 随机选择其中一个没有被访问到的对象p
- 标记p为被访问到了
- 如果p的半径领域至少有MinPts个对象,是核心对象
- 创建一个新簇C,并把p添加到C
- 遍历r邻域集合
- 如果某个点没有被标记,则标记为访问过了
- 将这些点添加到C
- 以这些添加到C里的点为中心发展下线
- 直到所有的下线都不是核心对象时停止
参数选择
- 半径r:可以根据K距离来设定:来找突变点
- K距离:给定数据集P={p(i); i=0,1,…n},计算点P(i)到集合D的子集S中所有点之间的距离,距离按照从小到大的顺序排序,d(k)就被称为k-距离。
- MinPts:一般取得小一些,多次尝试
DBSCAN算法优缺点
- 优势:
- 不需要指定簇个数
- 可以发现任意形状的簇
- 擅长找到离群点(检测任务)
- 两个参数就够了
- 劣势:
- 高维数据有些困难(可以做降维)
- 参数难以选择(参数对结果的影响非常大)
- Sklearn中效率很慢(数据削减策略)
可视化网址:
https://www.naftaliharris.com/blog/visualizing-k-means-clustering/
https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/

























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










