CPP数论专题

1.学习目的

数论是研究整数性质及其规律的一门基础数学学科，具有严密的逻辑结构和广泛的应用价值。通过学习数论，旨在：

1. 培养逻辑思维与严谨推理能力
   掌握数论中的基本定义、定理与证明方法，提升解决问题的抽象思维与数学表达能力。

2. 理解整数结构与整除性质
   深入学习整除、公因数与最小公倍数、同余理论、素数分布等基本概念，为进一步研究代数、密码学等打下基础。

3. 掌握数论算法与计算技巧
   熟悉欧几里得算法、模反元素求解、快速幂算法、中国剩余定理等经典算法，提升算法分析与编程实现能力。

4. 为现代应用打基础
   数论在密码学、区块链、计算机安全、编码理论等现代信息技术中有重要应用，学习数论有助于理解相关核心原理。

5. 拓展数学视野与学术基础
   通过学习初等数论与代数数论的基础内容，拓展对现代数学的认识，为进一步研究数学及其交叉学科提供理论支撑。

---

如需针对**不同方向（如竞赛、计算机、纯数学研究）**进一步个性化调整，我也可以继续完善。你希望这个用于哪种场合？

2.案例1

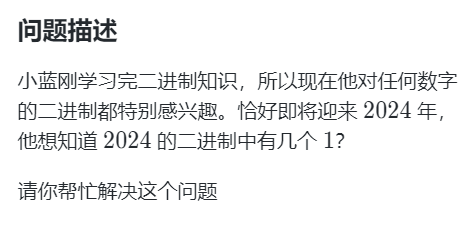
程序：

#include <iostream>
using namespace std;
int main()
{
  // 请在此输入您的代码
  int N=2024;
  int count = 0;
  while(N){
    if(N%2==1){
      count++;
    }
    N/=2;
  }
  cout << count <<endl;
  return 0;
}

2.案例2

程序：

#include <iostream>
using namespace std;
#include<cmath>
int main()
{
  // 请在此输入您的代码
  int N=2022;
  int res=0;
  int pos=0;
  while(N){

    res+= N % 10 * pow(9,pos);
    N/=10;
    ++pos;
    
  }
  cout<<res<<endl;
  return 0;
}

案例3–组合数

代码：

#include <iostream>
using namespace std;
long long C(long long n,long long m)
{
  if(m==1) return n;
  if(m==2) return n*(n-1)/2;
  if(m==3)  return n*(n-1)*(n-2)/6;
  if(m==4) return n*(n-1)*(n-2)*(n-3)/24;
  return -1;
}
int main()
{
  // 请在此输入您的代码
  long long n,k;
  cin>>n>>k;
  if(k==1) cout << 1 <<'\n';
  else if(k==2) cout << C(n,2)+1<<'\n';
  else if(k==3) cout << 2*C(n,3)+C(n,2)+1<<'\n';
  else cout << 9*C(n,4)+2*C(n,3)+C(n,2)+1<<'\n';
  return 0;
}