ADP&RL - 近似动态规划和强化学习 - Note 1 - Introduction

最新推荐文章于 2025-09-08 10:29:29 发布

原创

最新推荐文章于 2025-09-08 10:29:29 发布 · 2.3k 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #算法 #强化学习 #概率论

1. Intorduction

Abbreviations Declaration

SDM: sequential decision making 顺序决策
DP: Dynamic Programming 动态规划
MDP: Markov Decision Process 马尔科夫决策过程

这是在Quora上对动态规划(DP)说明的极好的例子

writes down “1+1+1+1+1+1+1+1 =” on a sheet of paper
“What’s that equal to?”
counting “Eight!”
writes down another “1+” on the left
“What about that?”
quickly “Nine!”
“How’d you know it was nine so fast?”
“You just added one more”
"So you didn’t need to recount because you remembered there were eight! Dynamic Programming is just a fancy way to say ‘remembering stuff to save time later’ "

这一部分是对被称为 memorization部分的的解释。

1.1 Decision making 决策

决策是人类或任何生物为了维持生存和存在而进行的最基本的活动。作为一个生存的决策者，他们在一个复杂的、未知的、不可预测的、不断变化的环境中不断遇到各种各样的挑战。为了应对这些挑战，应在评估情况或环境变化后作出相应的决定。可以说，做出正确决定的能力不是与生俱来的，但幸运的是，他们可以通过学习环境经验的过程获得。当然，获得这种学习能力往往伴随着一定的成本。也就是说，他们必须通过尝试各种决策，包括错误的决策来学习正确的决策，以对环境做出反应，接受环境的反馈，并在未来的决策中更新自己的策略。
例子， AlphaGo, Autonomous Driving

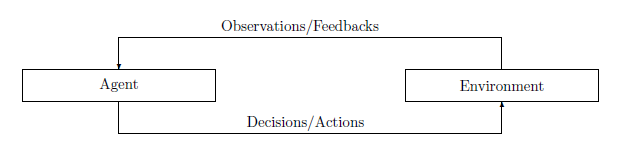
1.2 Modelling Sequential Decision Making

Definition 1.2 (Machine learning 机器学习).
机器学习是一个计算机程序，它 “关于某类任务 $\mathcal{T}$ ,从经验 $\mathcal{E}$ 中学习。它在 $\mathcal{T}$ 中的任务表现，由性能测量 $\mathcal{P}$ 度量，随着经验 $\mathcal{E}$ 的增加而提高”。

$\mathcal{X}$ ：状态空间，描述环境中所有情况的集合。
$\mathcal{U}$ ：可接受行动的集合。
$\mathcal{X}_k, \mathcal{U}_k$ : 初始时间点之后的第 $k$ 个状态或阶段的可接受的状态空间和行动空间。

Definition 1.3 历史（history ）或轨迹（trajectory ）被定义为环境的状态和智能体的交互而产生的行动的序列，即。
$:=(x_0,u_0,...,x_{N-1},u_{N-1},x_N) \in \mathcal{X}_0 \times \mathcal{U}_0 \times ... \times\mathcal{U}_{N-1} \times\mathcal{X}_N \tag{1.1}$
其中，
$N$ : 交互的范围（horizon of interaction）

而当 范围（horizon ） 是有限的，相应的SDM问题被称为有限范围问题（finite horizon problem） 或RL背景下的事件问题（episodic problem）。

为了使状态转换问题更具有可操作性，我们需要建立一个系统演化的模型 $(x_k, u_k) \to x_{k+1}$ 。在一个状态 $k$ ，环境和智能体之间的交互被描述为以下离散时间动态系统

$x_{k+1} = f_k(x_k, u_k, w_k), \text{for} \ k = 0,..., N-1 \tag{1.2}$

$w_k \in \mathcal{W}_k$ 表示阶段 $k$ 的扰动(perturbation) 或不确定性(uncertainty) 。

在状态 $k$ 的扰动可以由条件概率 $p(w_k|x_k, u_k)$ 驱动，而扰动往往要与历史无关，即 $p(w_k)$ 。我们用 $h$ 来表示轨迹或历史。在每个决策状态中，需要对轨迹 $h$ 进行适当的评估，以促进下一次决策。

Assumption 1.1 (Reinforcement hypothesis 强化假设).智能行为源于个人的行为，该行为寻求最大化其从环境中获得的奖励的积累。

具体来说，对于一个交互的基本部分（ $x_k, u_k, x_{k+1}$ ）来说，我们可以构建一个实值评价，即对于 $k = 0, . . ., N - 1$ 来说
$g_k= \mathcal{X}_k \times \mathcal{U}_k \times \mathcal{W}_k \to \mathbb{R},\\ (x_k, u_k, w_k) \to g_k(x_k, u_k, w_k). \tag{1.3}$

这是一个局部评估函数，对于一个基本的转换来说也被称为局部"成本去向函数（cost-to-go function） "，或者在RL文献中被称为 奖励函数（reward function）。

Remark 1.1 （Cost function vs. reward function 成本函数 vs. 奖励函数）
DP和RL的区别可以从成本函数的选择来看。DP中的成本函数通常是客观地预先确定的。但在RL中，成本函数更多的是由解决方案提供者或工程师手动设计的。

使用（1.3）中定义的基本评估和强化假设，我们可以定义整个轨迹的评估，其中包括所有的局部转换，即
$G(h):=g_N(x_N) + \sum_{k=0}^{N-1}g_k(x_k,u_k, w_k) \tag{1.4}$

其中 $g_N(x_N)$ 定义为在最终状态 $N$ 的的成本函数。为了使这种评估具有可比性，通常假设成本函数具有边界性。

Assumption 1.2 （Bounded cost function 有边界的成本函数）

成本函数 $g_k(x_k, u_k, w_k)$ 被假设为有边界, i.e., $|g_k(x_k, u_k, w_k)| < \infin \text{ for all } k = 0, ..., N-1$

用 $w :=[w_0, w_1, ... w_{N-1}]$ 表示整个范围上的扰动，用 $p (w)$ 表示 $w$ 的概率密度函数。因此，从一个给定的初始状态 $x_0\in \mathcal{X}_0$ 开始，跟随一连串的行动 $\pi:= {u_0, u_1, ..., u_{N-1}} \in \mathcal{U}_0 \times ... \times\mathcal{U}_{N-1}$