统计学习方法——第11章 条件随机场（CRF）

条件随机场（Conditional Random Field， CRF）是给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型，其特点是假设输出随机变量构成马尔科夫随机场。CRF主要用于不同的预测问题和标注问题。

     定义：设与是随机变量，是给定的条件下的条件概率分布。若随机变量构成一个由无向图表示的马尔科夫随机场，即：对任意结点成立，则条件概率分布为条件随机场。表示与结点有连接的所有结点，表示除结点以外的所有结点。

      举例：线性链条件随机场（linear chain CRF），设,均为线性链表示的随机变量序列，在给定随机变量序列的条件下随机变量序列的条件概率分布构成条件随机场，即满足马尔科夫性：

                                                    

概率无向图模型：

     概率无向图模型（probabilistic  undirected graphical model）又称马尔科夫随机场，是一个由无向图表示的联合概率分布；设有联合概率分布，是一组随机变量，无向图表示概率分布，即在图中，节点表示一个随机变量，边表示随机变量之间的概率依赖关系。

     成对马尔科夫性：

            设和是无向图中任意两个没有边连接的节点，节点和分别对应随机变量和，其他所有节点为,对应随机变量组,成对马尔科夫性是指在给定随机变量组条件下随机变量和相互独立。

 

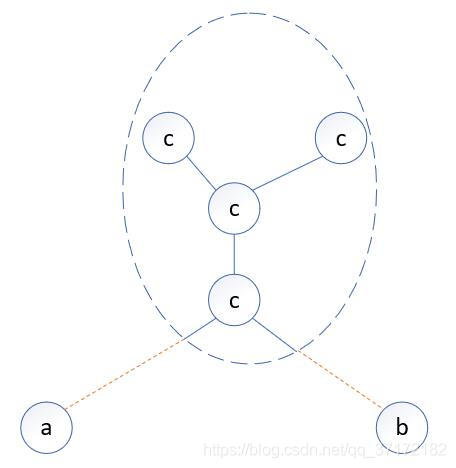
      局部马尔科夫性：

           设是无向图中任意一个节点，是与有边连接的所有节点，是除，以外的所有节点的。局部马尔科夫性是指在给定随机变量组的条件下随机变量和随机变量组相互独立。

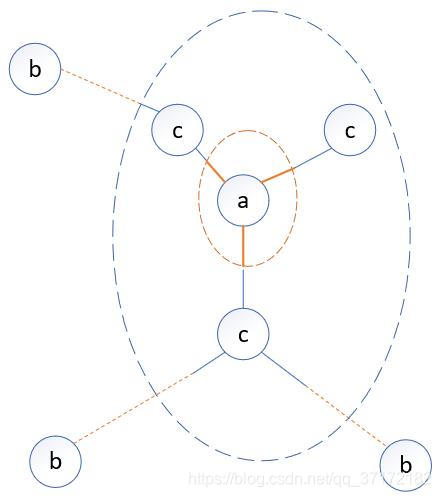
      全局马尔科夫性：

             设节点集合和是无向图中被节点集合分开的任意节点集合，全局马尔科夫性是指给定随机变量组的条件下随机       变量组和随机变量组相互独立。

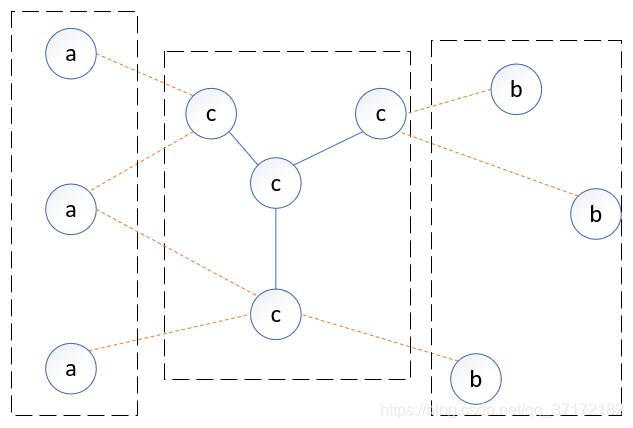
    因式分解：

     将概率无向图的联合概率分布表示为其最大团上的随机变量的函数的乘积的形式，称为概率无向图的因式分解。

     团与最大团：

     无向图中任意两个节点均有连接边的节点子集称为团（clique）。若是无向图中的一个团且不能加入中的任意一个节点构成最大团，则称为最大团（maximal clique）。

     给定概率无向图，是无向图的最大团，表示对应的随机变量，则概率无向图联合概率分布可以表示成所有最大团的函数的乘积的形式：  其中，为规范化因子，,函数称为势函数（potential function），势函数严格为正，通常定义为指数函数：

    线性链条件随机场参数化形式：

    设为线性链条件随机场，则在随机变量取值为的条件下，随机变量取值为时的条件概率有如下形式：

                      

     式中是特征函数，是对应的权重。