【c++&Leetcode】287. Find the Duplicate Number, 142. Linked List Cycle II

问题入口

 时间复杂度: O(n+k), 空间复杂度: O(1)

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int fast = 0, slow = 0;
        while (true)
        {
            fast = nums[nums[fast]];
            slow = nums[slow];

            if(fast == slow)
                break;
        }

        int slow2 = 0;
        while(true)
        {
            slow = nums[slow];
            slow2 = nums[slow2];
            if (slow == slow2)
                break;
        }
        return slow;
    }

};

时间复杂性

该函数使用Floyd的乌龟兔算法来检测链表中的循环。
该算法的时间复杂度为O（n+k），其中n是循环开始前的节点数，k是循环中的节点数。
第一个循环（乌龟和兔子运动）需要O（n）时间。
第二个循环（检测循环的开始）需要O（k）时间。
因此，总的时间复杂度为O（n+k）。

空间复杂性

空间复杂度为O（1），因为无论链表的大小如何，该算法都只使用恒定量的额外空间。
唯一使用的附加指针是slow、fast和slow2，它们都是常量。
总之，时间复杂度为O（n+k），空间复杂度为0（1），其中n是循环开始前的节点数，k是循环中的节点数。该算法有效地检测循环的开始，而不使用与链表大小成比例的额外空间。 

思想：Floyd's Tortoise and Hare

这个算法除了可以检测是否有环（Leetcode 141），还可以用来检测重复数。当然这还需要一个慢指针才能实现。具体请点击标题跳转到原视频，这里是把内容再梳理一遍。如果有不对的地方请多多指教。

这道题的索引和数组取值范围是相关联的。比如长度为5的数组，元素会在[1,4]这个区间。这就可以将索引视为指针，元素视为地址，画出下面这样的图进而观察到重复数的特点。可以发现，重复数会有两个箭头指向它。

这也就意味着，如果从不同方向的两个起点出发都是可以到达重复数的位置。如果两个起点和重复数位置的距离一样的话，那么两个指针一起从起点处出发必然可以相遇，而相遇的位置正好就是重复数的位置。

起点1就是从索引0处开始。那么起点2该如何找到呢？Floyd's Tortoise and Hare算法就派上了用场。快慢指针同时从索引0处出发，它们第一次相遇的位置就是起点2。

这里作者很贴心地举了一个例子帮助大家理解。如下图，两个指针走了三次后最终在3处相遇。

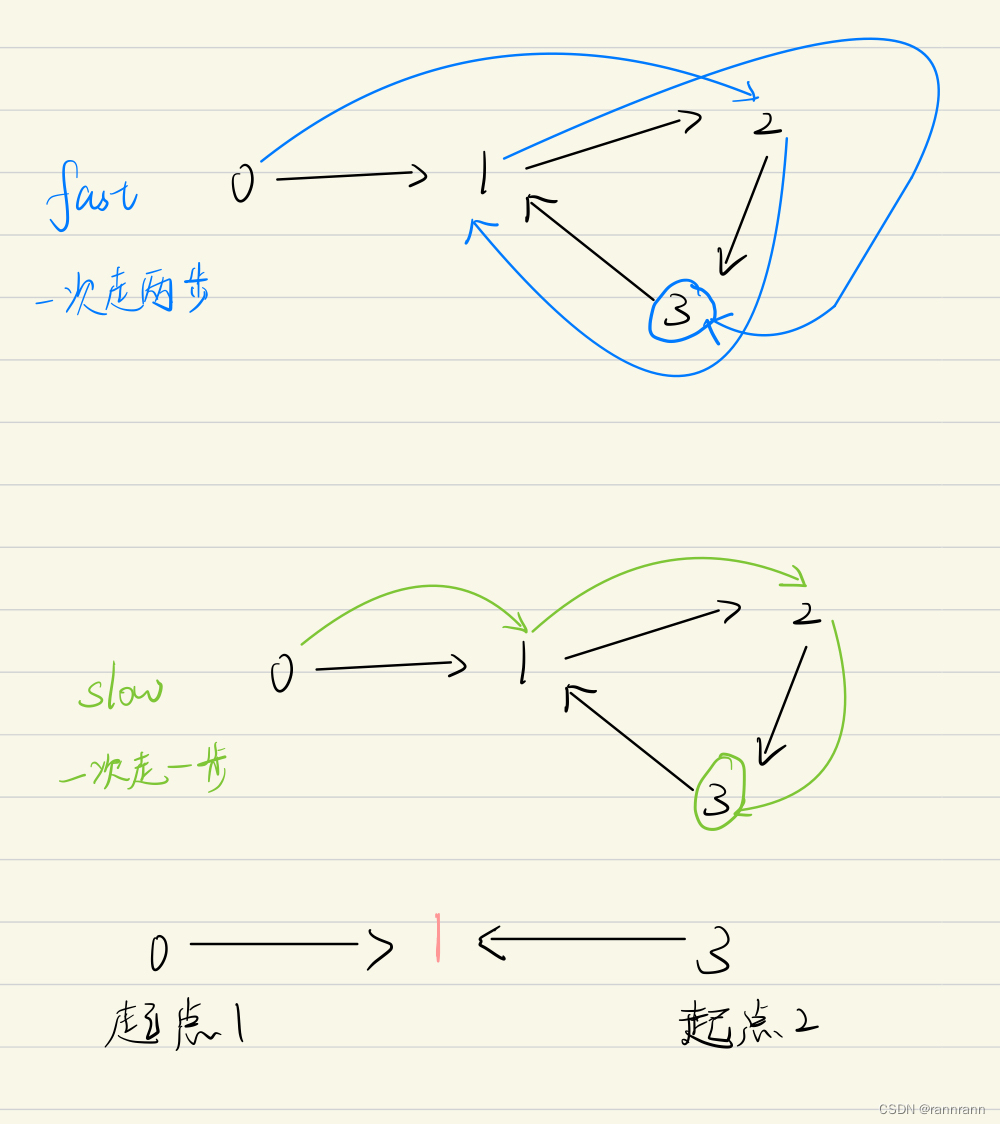
可以看到0和3都和重复数1相差一步。

找到起点2之后我们可以再让一个慢指针从0处出发，两个慢指针同时出发，相遇的位置即重复数。

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int fast = 0, slow = 0;
        while (true)
        {
            fast = nums[nums[fast]];
            slow = nums[slow];

            if(fast == slow)
                break;
        }

        int slow2 = 0;
        while(true)
        {
            slow = nums[slow];
            slow2 = nums[slow2];
            if (slow == slow2)
                break;
        }
        return slow;
    }

};

至于为什么这个结论能够成立，作者通过代数证明。

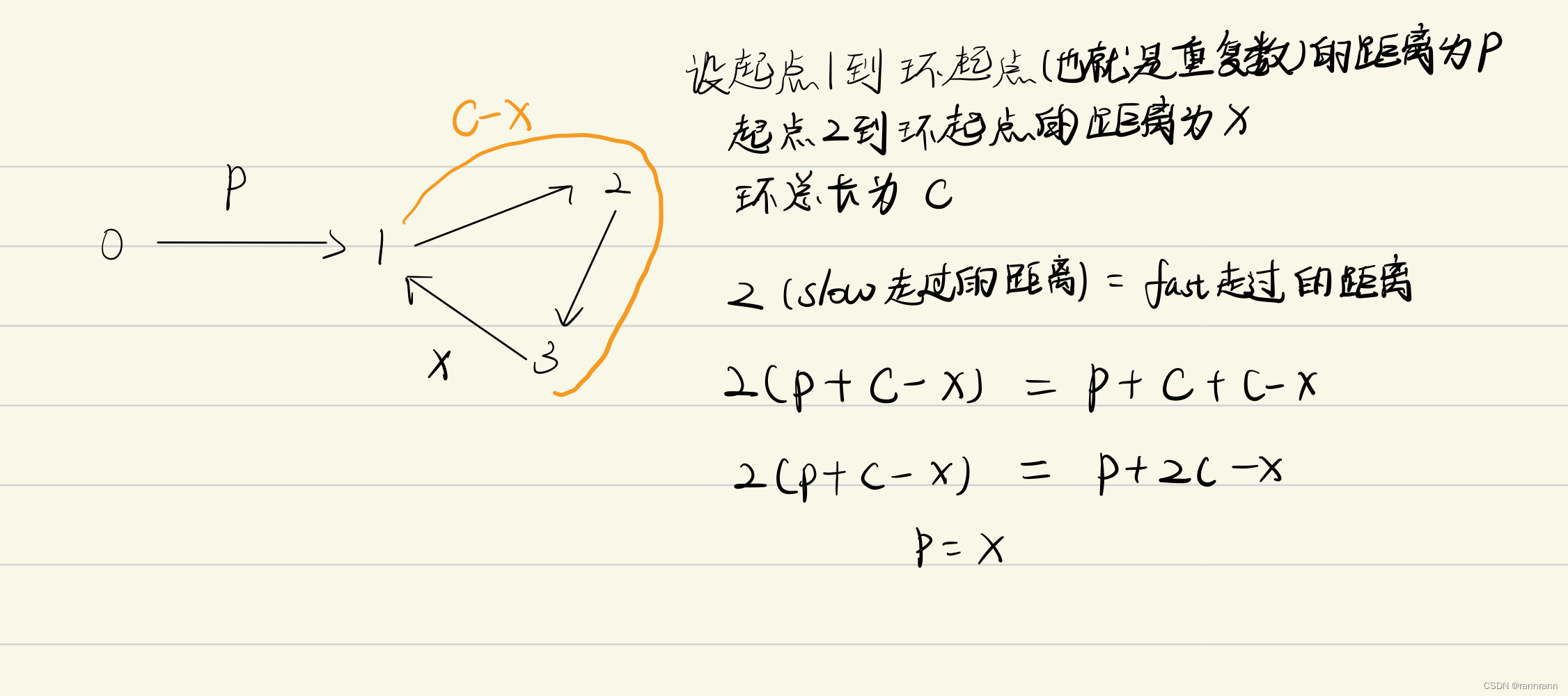
 my way

题目虽然要求不要更改原数组，但是我还是通过复制给数组排序，然后通过遍历返回重复数。这样做就是时间超时，不过好处是复习了排序算法（另外bb一句，印度人讲算法真的强）。