Matlab绘制分形图——正方形

分形几何是一门几何学，例如雪花等结构其微观的几何形状与宏观的几何形状具有相似性，利用这种相似性可以将局部的结构组合起来。由于许多分形现象都是在自然界中观察到的，因此分形几何学又被称为描述大自然的几何学。

正方形是一种简单的几何图形，利用正方形的各种组合，可以绘制出许多漂亮的图案。

例如将正方形的一个边上分为两段，两段长度保持一定比例，一次组成多个正方形，可以形成多个图案，如下图所示：

调整两侧正方形的边长和颜色，比如用正方形的边长作为正方形颜色选择的依据，可以绘制如下的树的图案：

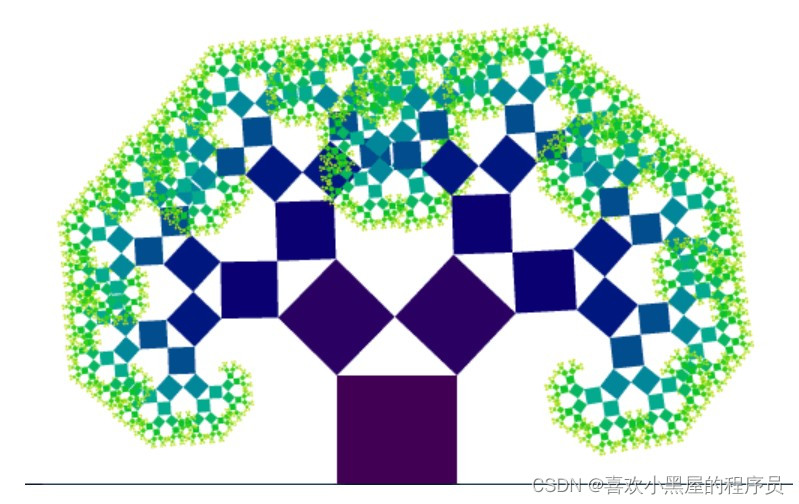
以下是该分形图的Matlab代码：

clc,clear
% 初始正方形边长
Length_Cube=1;
Location=[0 0 Length_Cube 0];B=Location;
% 分形角度
t=36/180*pi;
% 分形阶数
Num=14;
% 最小正方形边长
LengthMin=0.05;
% 颜色
Color=[1 0 0;0 1 0;0 0 1;1 1 0];
for i=1:Num
    Location=B;
    B=[];
    Bindex=1;
    for k=1:size(Location,1)
        x(1,1)=Location(k,1);
        x(2,1)=Location(k,1)+Location(k,3)*cos(Location(k,4));
        x(3,1)=Location(k,1)+Location(k,3)*cos(Location(k,4))-Location(k,3)*sin(Location(k,4));
        x(4,1)=Location(k,1)-Location(k,3)*sin(Location(k,4));
        x(5,1)=Location(k,1);
        
        y(1,1)=Location(k,2);
        y(2,1)=Location(k,2)+Location(k,3)*sin(Location(k,4));
        y(3,1)=Location(k,2)+Location(k,3)*sin(Location(k,4))+Location(k,3)*cos(Location(k,4));
        y(4,1)=Location(k,2)+Location(k,3)*cos(Location(k,4));
        y(5,1)=Location(k,2);
        pc=ceil(rand(1,1)*size(Color,1));
        if k<size(Location,1)
           if Location(k,3)>LengthMin && Location(k+1,3)>LengthMin
           patch(x,y,Color(pc,:))
           end
        else
            patch(x,y,Color(pc,:))
        end
        B(Bindex,1)=x(4,1);
        B(Bindex,2)=y(4,1);
        B(Bindex,3)=sqrt((y(2,1)-y(1,1))^2+(x(2,1)-x(1,1))^2)*cos(t);
        B(Bindex,4)=atan((y(2,1)-y(1,1))/(x(2,1)-x(1,1)))+t;
        u=[x(2,1)-x(1,1),y(2,1)-y(1,1)];e=[1 0];
        tk=acos(u*e'/sqrt(u(1,1)^2+u(1,2)^2));
        if u(1,1)<0 && u(1,2)<0 
            tk=2*pi-tk;
        elseif u(1,1)>0 && u(1,2)<0 
            tk=2*pi-tk;
        elseif u(1,1)==0 && u(1,2)<0 
            tk=1.5*pi;
        end
        B(Bindex,4)=tk+t;
        Bindex=Bindex+1;
        B(Bindex,1)=x(4,1)+B(Bindex-1,3)*cos(B(Bindex-1,4));
        B(Bindex,2)=y(4,1)+B(Bindex-1,3)*sin(B(Bindex-1,4));
        B(Bindex,3)=sqrt((y(2,1)-y(1,1))^2+(x(2,1)-x(1,1))^2)*sin(t);
        B(Bindex,4)=atan((y(2,1)-y(1,1))/(x(2,1)-x(1,1)))+t-pi/2;
        u=[x(2,1)-x(1,1),y(2,1)-y(1,1)];e=[1 0];
        tk=acos(u*e'/sqrt(u(1,1)^2+u(1,2)^2));
         if u(1,1)<0 && u(1,2)<0 
            tk=2*pi-tk;
        elseif u(1,1)>0 && u(1,2)<0 
            tk=2*pi-tk;
        elseif u(1,1)==0 && u(1,2)<0 
            tk=1.5*pi;
        end
        B(Bindex,4)=tk+t-pi/2;
        Bindex=Bindex+1;
    end
 
end
axis equal