查找算法---数据结构

相关概念

1.1 静态查找和动态查找

  静态查找：数据集合稳定，不需要添加，删除元素的查找操作。

  动态查找：数据集合在查找的过程中需要同时添加或删除元素的查找操作。

1.2 查找结构

  对于静态查找来说，我们不妨可以用线性表结构组织数据，这样可以使用顺序查找算法，如果我们再对关键字进行排序，则可以使用折半查找算法或斐波那契查找算法等来提高查找的效率。

  对于动态查找来说，我们则可以考虑使用二叉排序树的查找技术，另外我们还可以使用散列表结构来解决一些查找问题，这些技术我们都将在这部分教程里边介绍给大家。

2. 顺序查找

2.1 思路

  顺序查找又叫线性查找，是最基本的查找技术，它的查找过程是：从第一个（或者最后一个）记录开始，逐个进行记录的关键字和给定值进行比较，若某个记录的关键字和给定值相等，则查找成功。如果查找了所有的记录仍然找不到与给定值相等的关键字，则查找不成功。

2.2 代码

  首先是一种最直觉的实现方法

// 顺序查找，a为要查找的数组，n为要查找的数组的长度，key为要查找的关键字
int Sq_Search(int *a, int n, int key)       //其中的 *a 的含义是数组的头指针，传入头指针相当于传入了这个数组
{
    int i;
    for( i=1; i <= n; i++ )
    {
        if( a[i] == key )
        {
            return i;
        }
    }
    return 0;
}

但是上面这段代码的复杂度是 O(2n) ，那有每一种复杂度为 n 的查找代码呢？有的，如下优化方案

// 顺序查找优化方案，a为要查找的数组，n为要查找的数组的长度，key为要查找的关键字
int Sq_Search(int *a, int n, int key)
{
    int i = n;
    a[0] = key
    while( a[i] != key )
    {
        i--;
    }

    return i;
}

这个算法虽然复杂度只有 n ，但是同样存在着一个问题，就是它对于里面具有多个相同的数的情况是没有考虑在内的。

2.3 相关思考题

  假设以下有一个结构体存放的是学生的记录，每条记录包括：学号、姓名、成绩，请编写一个程序，要求输出1024编号同学的具体信息。 

 

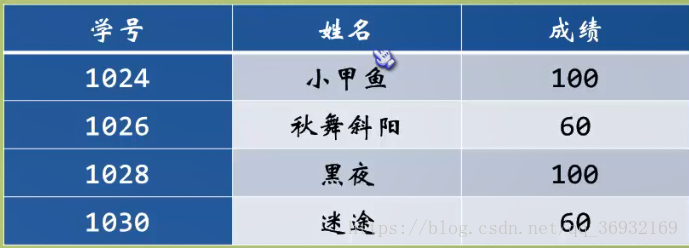
2.3.1 代码

#include <stdio.h>

typedef struct student
{
    int id;
    char name[10];
    float score;
}Student;

float search(Student stu[], int n, int key)
{
    int i;

    for( i=0; i < n; i++ )
    {
        if( stu[i].id == key )
        {
            return i.score;
        }
    }

    return -1;
}

int main()
{
    Student stu[4] = {
        {1024, "小甲鱼", 100}, 
        {1026, "秋舞斜阳", 60}, 
        {1028, "黑夜", 100}, 
        {1030, "迷途", 60}
        };

    float score;

    score = search(stu, 4, 1024);
    printf("1024号童鞋的成绩是：%f", score);

    return 0;
}

3. 折半查找

  如果从文件中读取的数据记录的关键字是有序排列的，则可以用一种效率比较高的查找方法来查找文件的记录，这就是折半查找法，又称为二分法搜索。

3.1 基本思想

  减小查找序列的长度，分而治之地进行关键字的查找。先确定待查找记录的所在范围，然后逐渐缩小这个范围，直到找到该记录或查找失败（查无该记录）为止。

  例如有序列：1 1 2 3 5 8 13 21 34 55 89（该序列包含 11 个元素，而且关键字单调递增。），现要求查找关键字 key 为 55 的记录。我们可以设指针 low 和 high 分别指向关键字序列的上界和下界，指针 mid 指向序列的中间位置，即 mid = (low+high)/2。如下图所示 

首先将 mid 所指向的元素与 key 进行比较，因为我们这里 key = 55，大于 8，这就说明待查找的关键字一定位于 mid 和 high 之间。于是我们执行 low = mid+1; mid = (low+high)/2;如下图所示 

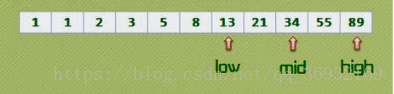
然后再将 mid 所指的 34 与 key 进行比较，仍然 mid < key，所以继续执行 low = mid+1; mid = (low+high)/2;如下图所示 

 

接下来仍然将 mid 所指的元素与 key 进行比较，结果相等，查找成功。返回 mid 的指针值，程序结束。假设我们要查找的关键字 key = 88，那么上述的查找还要继续进行下去 low = mid+1; mid = (low+high)/2;如下图所示 

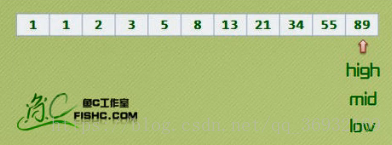
时间复杂度O(log2(n))

3.2 迭代实现

#include <stdio.h>

int bin_search( int str[], int n, int key )
{
        int low, high, mid;

        low = 0;
        high = n-1;

        while( low <= high )
        {
                mid = (low+high)/2;
                if( str[mid] == key )
                {
                        return mid;                // 查找成功
                }
                if( str[mid] < key )
                {
                        low = mid + 1;        // 在后半序列中查找
                }
                if( str[mid] > key )
                {
                        high = mid - 1;        // 在前半序列中查找
                }
        }

        return -1;                                // 查找失败
}

int main()
{
        int str[11] = {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89};
        int n, addr;

        printf("请输入待查找的关键字: ");
        scanf("%d", &n);

        addr = bin_search(str, 11, n);
        if( -1 != addr )
        {
                printf("查找成功， 关键字 %d 所在的位置是: %d\n", n, addr);
        }
        else
        {
                printf("查找失败!\n");
        }

        return 0;
}

3.3 递归实现

#include<stdio.h>
#define SIZE 10
typedef int ElemType;
int refind(ElemType *data,int begin,int end,ElemType num);
int main(void){
            ElemType data[SIZE]={10,20,30,40,50,60,70,80,90,100};
            ElemType num;
            for(int i = 0;i<SIZE;i++)
                    printf("%d ",data[i]);
            printf("\n请输入要查找的数据:\n");
            scanf("%d",&num);
            int flag = refind(data,0,SIZE,num);
            printf("位置为:%d\n",flag);
            return 0;
}
/
//递归
int refind(ElemType *data,int begin,int end,ElemType num)
{
            if(begin > end)
            {
                      printf("没找到\n");
                      return -1;
             }

             int mid = (begin+end)/2;

             if(data[mid] == num)
            {
                      return mid;
             }else if(data[mid] <= num)
                      return refind(data,mid+1,end,num);
             else
                      return refind(data,begin,mid-1,num);
}

4. 插值查找（按比例查找）

  在上面的折半查找法中，每次都是对折之后再查找，但是实际上是可以不进行对折查找。比如说，我们在英语字典中查找某一个英语单词，首先会翻到这个单词的首字母的位置再进行查找，这种查找方式就叫做按比例查找。

4.1 基本思想

前提是均匀的一组有序数，这样比例才明显。 

它的基本思想就是，根据关键之在数组中的位置来确定 mid 的位置。

按照比例：假如low=1,high=100,key=60,a[low]=2,a[high]=102

 mid = low + ((key-a[low])/(a[high]-a[low]))*(high-low);

mid=1+((60-2)/(102-2))*(101-1)=1+60=61

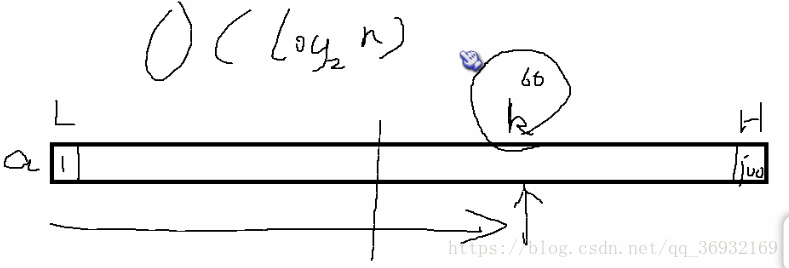
复杂度O(log2(n))

4.2 代码

#include <stdio.h>

int bin_search( int str[], int n, int key )
{
    int low, high, mid;

    low = 0;
    high = n-1;

    while( low <= high )
    {
        mid = low + ((key-a[low])/(a[high]-a[low]))*(high-low); // 插值查找的唯一不同点
        //按照比例取到最接近的位置
        if( str[mid] == key )
        {
            return mid;              
        }
        if( str[mid] < key )
        {
            low = mid + 1;       
        }
        if( str[mid] > key )
        {
            high = mid - 1;       
        }
    }

    return -1;                      
}

int main()
{
    int str[11] = {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89};
    int n, addr;

    printf("请输入待查找的关键字: ");
    scanf("%d", &n);

    addr = bin_search(str, 11, n);
    if( -1 != addr )
    {
        printf("查找成功，可喜可贺，可口可乐! 关键字 %d 所在的位置是: %d\n", n, addr);
    }
    else
    {
        printf("查找失败!\n");
    }

    return 0;
}

5. 斐波那契查找（黄金分割法查找）

  我们知道黄金分割比是0.618:1，但是这个比例实际上和斐波那契数列也是有关系的，

斐波那契数列，又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、····，在数学上，斐波那契被递归方法如下定义：F(1)=1，F(2)=1，F(n)=f(n-1)+F(n-2) （n>=2）。该数列越往后相邻的两个数的比值越趋向于黄金比例值（0.618）。

  5.1 基本思想

     斐波那契查找就是在二分查找的基础上根据斐波那契数列进行分割的。在斐波那契数列找一个等于略大于查找表中元素个数的数F[n]，将原查找表扩展为长度为F[n](如果要补充元素，则补充重复最后一个元素，直到满足F[n]个元素)，完成后进行斐波那契分割，即F[n]个元素分割为前半部分F[n-1]个元素，后半部分F[n-2]个元素，找出要查找的元素在那一部分并递归，直到找到。

     斐波那契查找的时间复杂度还是O(log 2 n )，但是 与折半查找相比，斐波那契查找的优点是它只涉及加法和减法运算，而不用除法，而除法比加减法要占用更多的时间，因此，斐波那契查找的运行时间理论上比折半查找小，但是还是得视具体情况而定。

     对于斐波那契数列：1、1、2、3、5、8、13、21、34、55、89……（也可以从0开始），前后两个数字的比值随着数列的增加，越来越接近黄金比值0.618。比如这里的89，把它想象成整个有序表的元素个数，而89是由前面的两个斐波那契数34和55相加之后的和，也就是说把元素个数为89的有序表分成由前55个数据元素组成的前半段和由后34个数据元素组成的后半段，那么前半段元素个数和整个有序表长度的比值就接近黄金比值0.618，假如要查找的元素在前半段，那么继续按照斐波那契数列来看，55 = 34 + 21，所以继续把前半段分成前34个数据元素的前半段和后21个元素的后半段，继续查找，如此反复，直到查找成功或失败，这样就把斐波那契数列应用到查找算法中了。

       数组a的长度其实很好估算，比如你定义了有10个元素的有序数组a[20]，n=10，那么n就位于8和13，即F[6]和F[7]之间，所以k=7，此时数组a的元素个数要被扩充，为：F[7] - 1 = 12个； 再如你定义了一个b[20]，且b有12个元素，即n=12,那么很好办了，n = F[7]-1 = 12, 用不着扩充了； 又或者n=8或9或11，则它一定会被扩充到12； 再如n=13，最后得出n位于13和21，即F[7]和F[8]之间，此时k=8，那么F[8]-1 = 20,数组a就要有20个元素了。 所以，n = x（13<=x<=20）时，最后都要被扩充到20；类推，如果n=25呢，则数组a的元素个数肯定要被扩充到 34 - 1 = 33个（25位于21和34，即F[8]和F[9]之间，此时k=9，F[9]-1 = 33），所以，n = x（21<=x<=33）时，最后都要被扩充到33。也就是说，最后数组的元素个数一定是（某个斐波那契数 - 1），这就是一开始说的n与F[k]-1的关系。

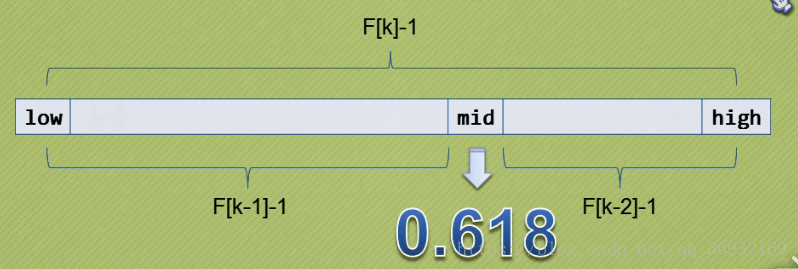
        对于二分查找，分割是从mid=(low+high)/2开始；而对于斐波那契查找，分割是从mid = low + F[k-1] - 1开始的； 通过上面知道了，数组a现在的元素个数为F[k]-1个，即数组长为F[k]-1，mid把数组分成了左右两部分， 左边的长度为：F[k-1] - 1， 那么右边的长度就为（数组长-左边的长度-1）， 即：（F[k]-1） - （F[k-1] - 1） = F[k] - F[k-1] - 1 = F[k-2] - 1。
斐波那契查找的核心是：
1）当key=a[mid]时，查找成功；
2）当key<a[mid]时，新的查找范围是第low个到第mid-1个，此时范围个数为F[k-1] - 1个，即数组左边的长度，所以要在[low, F[k - 1] - 1]范围内查找；
3）当key>a[mid]时，新的查找范围是第mid+1个到第high个，此时范围个数为F[k-2] - 1个，即数组右边的长度，所以要在[F[k - 2] - 1]范围内查找。

 

   关于斐波那契查找， 如果要查找的记录在右侧，则左侧的数据都不用再判断了，不断反复进行下去，对处于当众的大部分数据，其工作效率要高一些。所以尽管斐波那契查找的时间复杂度也为O(logn)，但就平均性能来说，斐波那契查找要优于折半查找。可惜如果是最坏的情况，比如这里key=1，那么始终都处于左侧在查找，则查找效率低于折半查找。

   还有关键一点，折半查找是进行加法与除法运算的（mid=(low+high)/2），插值查找则进行更复杂的四则运算（mid = low + (high - low) * ((key - a[low]) / (a[high] - a[low]))），而斐波那契查找只进行最简单的加减法运算（mid = low + F[k-1] - 1），在海量数据的查找过程中，这种细微的差别可能会影响最终的效率。

 

首先要明确：如果一个有序表的元素个数为n,并且n正好是（某个斐波那契数 - 1），即n=F[k]-1时，才能用斐波那契查找法。 如果有序表的元素个n不等于（某个斐波那契数 - 1），即n≠F[k]-1，这时必须要将有序表的元素扩展到大于n的那个斐波那契数 - 1才行，这段代码：

5.2 代码

#include <stdio.h>
#define MAXSIZE 20

void fibonacci(int *f)   //使用递推关系生成斐波那契数列
{
    int i;

    f[0] = 1;
    f[1] = 1;

    for(i=2; i < MAXSIZE; ++i)
    {
        f[i] = f[i-2] + f[i-1];

    }
}//f[i]  1 1 2 3 5 8 13 21 34 55 89
 // i    0 1 2 3 4 5 6  7  8  9  10 

// *a 是待查找数组的头指针，key 待查找的数字，n 是待查找数组中元素的个数
a[i]  1, 5, 15, 22, 25, 31, 39, 42, 47, 49, 59, 68, 88
//若 key=39 n=13
int fibonacci_search(int *a,int key,int n)
{
    int low = 0;
    int high = n - 1;//high=13-1  下标从0开始
    int mid = 0;
    int k = 0;
    int F[MAXSIZE];
    int i;

    fibonacci(F);

   //计算n位于斐波那契数列的位置 
    while( n > F[k]-1 ) 
    {
        ++k;
    }
  
    //如果数组的长度小于对应的斐波那契数列中元素的值，那么将他用最大值拓展
    // 补充的元素值为最后一个元素的值
    //将a的元素扩展到(某斐波那契数 - 1)，即F[k]-1 
    for( i=n; i < F[k]-1; ++i) 
    {
        a[i] = a[high];
    }

    while( low <= high )
      {     // low：起始位置 0
			// 前半部分有f[k-1]个元素，由于下标从0开始
			// 则-1 获取 黄金分割位置元素的下标
   
        mid = low + F[k-1] - 1;//计算当前分割的下标 
        if( a[mid] > key )//a[5]=31
        {
           // 查找前半部分，高位指针移动
            high = mid - 1;
           // （全部元素） = （前半部分）+（后半部分）
		   // f[k] = f[k-1] + f[k-2]
		   // 因为前半部分有f[k-1]个元素，所以 k = k-1    
            k = k - 1;
        }
        else if( a[mid] < key )//a[5]=31<39
        {
            // 查找后半部分，高位指针移动
            low = mid + 1;
           // （全部元素） = （前半部分）+（后半部分）
		   // f[k] = f[k-1] + f[k-2]
		   // 因为后半部分有f[k-2]个元素，所以 k = k-2
            k = k - 2;
        }
        else
        {
            if( mid <= high ) 
            {
                //若相当则说明mid即为查找到的位置 
                return mid;
            }
            else
            {
             //若mid>n则说明是扩展的数值，返回n
                return high;
            }
        }
    }

    return -1;
}

int main()
{

    int a[MAXSIZE] = {1, 5, 15, 22, 25, 31, 39, 42, 47, 49, 59, 68, 88};
    int key;
    int pos;

    printf("请输入要查找的数字:");
    scanf("%d", &key);

    pos = fibonacci_search(a, key, 13);

    if( pos != -1 )
    {
        printf("\n查找成功，关键字 %d 所在的位置是: %d\n\n", key, pos);
    }
    else
    {
        printf("\未在数组中找到元素:%d\n\n", key);
    }

    return 0;
}