YOLOV3 Anchor Function

最新推荐文章于 2025-06-15 13:56:53 发布

graph builder

最新推荐文章于 2025-06-15 13:56:53 发布

阅读量710

点赞数

CC 4.0 BY-SA版权

分类专栏： # YOLO

本文链接：https://blog.youkuaiyun.com/qq_36783816/article/details/96441617

YOLO 专栏收录该内容

5 篇文章

订阅专栏

本文详细介绍了KMeans聚类算法及其在Anchor机制中的应用。KMeans算法是一种基于距离的聚类方法，用于将对象划分为多个簇。文章还探讨了Anchor机制在目标检测中的作用，包括Anchor的计算方法及在YOLO系列模型中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言：最近在学习anchor，下面是一些记录。
目录

1、Kmeans算法

1.1 Kmeans理解

K-means算法是很典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。

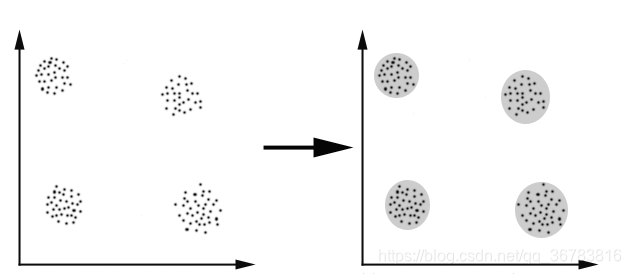
K-Means算法主要解决的问题如下图所示。我们可以看到，在图的左边有一些点，我们用肉眼可以看出来有四个点群，K-Means算法被用来找出这几个点群。

1.2 Kmeans原理

假定给定数据样本 $X$ ，包含了 $n$ 个对象 $X=\left \{ X_{1},X_{2},X_{3},...,X_{n} \right \}$ ，其中每个对象都具有 $m$ 个维度的属性。Kmeans算法的目标是将 $n$ 个对象依据对象间的相似性聚集到指定的 $k$ 个类簇中，每个对象属于且仅属于一个其到类簇中心距离最小的类簇中。对于Kmeans，首先需要初始化 $k$ 个聚类中心 $\left \{ C_{1},C_{2},C_{3},...,C_{k} \right \},1<k<=n$ ，然后通过计算每一个对象到每一个聚类中心的欧式距离，如下式所示：

$dis(X_{i},C_{i})=\sqrt{\sum_{t=1}^{m}(X_{it}-C_{it})^{2}}$

上式中， $X_{i}$ 表示第 $i$ 个对象 $1\leq i\leq n$ ， $C_{j}$ 表示第 $j$ 个聚类中心的 $1\leqslant j\leq k，X_{it}$ 表示第 $i$ 个对象的第 $t$ 个属性， $1\leqslant t\leq m，C_{jt}$ 表示第 $j$ 个聚类中心的第 $t$ 个属性。
依次比较每一个对象到每一个聚类中心的距离，将对象分配到距离最近的聚类中心的类簇中，得到 $k$ 个类簇 $\left \{ S_{1},S_{2},S_{3},...,S_{k}, \right \}$ 。

Kmeans算法用中心定义了类簇的原型，类簇中心就是类簇内所有对象在各个维度的均值，其计算公式如下
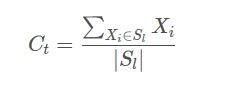
Ct=∑Xi∈SlXi∣Sl∣Ct=∣Sl∣∑Xi∈SlXi
式中， $C_{l}$ 表示第 $l$ 个聚类的中心， $1\leq l\leq k$ ， $\left | S_{l} \right |$ 表示第 $l$ 个类簇中对象的个数， $X_{i}$ 表示第 $l$ 个类簇中第 $i$ 个对象， $1\leq i\leq \left | S_{l} \right |$ 。

例如：
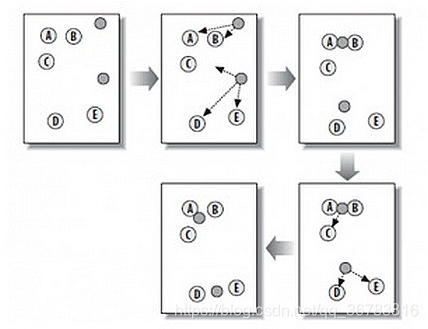
在这里插入图片描述
从上图中，我们可以看到，A, B, C, D, E 是五个在图中点。而灰色的点是我们的种子点，也就是我们用来找点群的点。有两个种子点，所以K=2。
K-Means的算法如下：
1). 随机在图中取K（这里K=2）个种子点。
2). 然后对图中的所有点求到这K个种子点的距离，假如点Pi离种子点Si最近，那么Pi属于Si点群。（上图中，我们可以看到A,B属于上面的种子点，C,D,E属于下面的种子点）
3). 接下来，我们要移动种子点到属于他的“点群”的中心。（见图上的第三步）
4). 然后重复第2）和第3）步，直到种子点没有移动（我们可以看到图中的第四步上面的种子点聚合了A,B,C，下面的种子点聚合了D，E）。

缺点：
需要提前指定k；
对种子点的初始化非常敏感。

2、Anchor机制

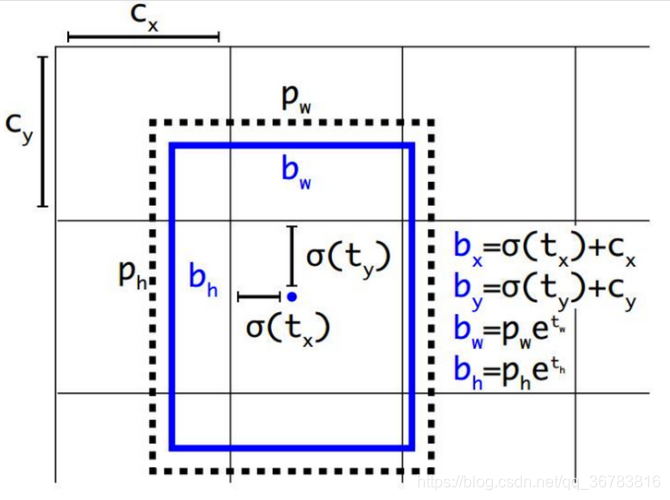
在这里插入图片描述
网络实际的预测值为tx、ty、tw、th，根据上图中的四个公式计算得到预测框的中心点坐标和宽高bx、by、bw、bh。其中，cx、cy为当前grid相对于左上角grid偏移的grid数量。σ()函数为logistic函数，将坐标归一化到0-1。最终得到的bx，by为归一化后的相对于grid cell的值。pw、 ph为与ground truth重合度最大的anchor的宽和高。实际使用中，作者为了将bw，bh也归一化到0-1，程序中的 pw，ph为anchor的宽、高和feature map的宽、高的比值。最终得到的bw，bh为归一化后相对于anchor的值。

3、Anchor计算

YOLOV3的默认 anchor box 尺寸是基于COCO训练集，使用 k-means 聚类算法获得的。
聚类的目的是anchor boxes和临近的ground truth有更大的IOU，因为使用欧氏距离会让大的bounding boxes比小的bounding boxes产生更多的error，而我们希望能通过anchor boxes获得好的IOU scores，并且IOU scores是与box的尺寸无关的。
为此作者定义了新的距离公式：

d(box,centroid)=1-IOU(box,centroid)

这样就保证距离越小，IOU值越大。

计算过程：

a. 使用的聚类原始数据是只有标注框的检测数据集，YOLOv2、v3都会生成一个包含标注框位置和类别的 txt 文件，其中每行都包含 $(x_j,y_j,w_j,h_j),j\in\{1,2,...,N\}$ ，即ground truth boxes相对于原图的坐标， $x_j,y_j)$ 是框的中心点， $w_j,h_j)$ 是框的宽和高， $N$ 是所有标注框的个数；
b. 首先给定 $k$ 个聚类中心点 $(W_i,H_i),i\in\{1,2,...,k\}$ ，这里的 $W_i,H_i$ 是anchor boxes的宽和高尺寸，由于anchor boxes位置不固定，所以没有 $(x, y)$ 的坐标，只有宽和高；
c. 计算每个标注框和每个聚类中心点的距离d=1-IOU(标注框,聚类中心)，计算时每个标注框的中心点都与聚类中心重合，这样才能计算IOU值，即
$d=1-IOU\left [ (x_j,y_j,w_j,h_j),(x_j,y_j,W_i,H_i) \right ]$ ，
$j\in\{1,2,...,N\},i\in\{1,2,...,k\}$ ，
将标注框分配给“距离”最近的聚类中心；
d. 所有标注框分配完毕以后，对每个簇重新计算聚类中心点，计算方式为 $W_i^{'}=\frac{1}{N_i}\sum w_{i},H_i^{'}=\frac{1}{N_i}\sum h_{i}，N_i$ 是第i个簇的标注框个数，就是求该簇中所有标注框的宽和高的平均值。重复第c、d，直到聚类中心改变量很小。

为什么YOLOv2和YOLOv3的anchor大小有明显区别？
如下是作者自己的解释：

So YOLOv2 I made some design choice errors, I made the anchor box size be relative to the feature size in the last layer. Since the network was down-sampling by 32. This means it was relative to 32 pixels so an anchor of 9x9 was actually 288px x 288px.
In YOLOv3 anchor sizes are actual pixel values. this simplifies a lot of stuff and was only a little bit harder to implement
https://github.com/pjreddie/darknet/issues/555#issuecomment-376190325

代码实现：

./darknet detector calc_anchors data/obj.data -num_of_clusters 9 -width 416 -height 416

python AlexeyAB/darknet/scripts/gen_anchors.py

注释

4、背景知识

anchor先是出现在Faster R-CNN，然后yolov2中折中选取5个anchor，yolov3采用9个anchor，提高了IOU。