练习杨辉三角

下面编写直角三角形的杨辉三角，用二维数组来a[i][j]来存储。首先来分析一下他的特点：
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1

1 j == 0 和 i == j的时候都是 1
2 其他位置上都是上面那个数和左上那个数 之和

#include<stdio.h>
#define N 10
int main(void)
{
	int i,j;
	int a[N][N] = {0};
	for(i=0; i<N; ++i)
	{
		for(j=0; j<N; ++j)
		{
			if((0 == j) || (i == j))
			{
				a[i][j] = 1;
			}
			else
			{
				a[i][j] = a[i-1][j] + a[i-1][j-1];
			}
		}
	}
	for(i=0; i<N; ++i)
	{
		for(j=0; j<N; ++j)
		{
			printf("%-3d\x20", a[i][j]);
		}
		printf("\n");
	}
	return 0;
}

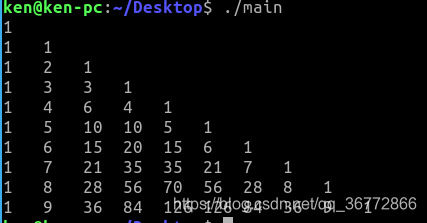
优化代码，因为我们只需要输出一半的数据，所以我们在赋值的时候可以写成 j<=i,而不是 j<N;

#include<stdio.h>
#define