核心思路:由果索因
一. 直观理解
1. 问题描述
对于如"图1"式(等式约束优化问题, 可行域是边界), 转化成拉格朗日乘子法的思路来源:
图1: 拉格朗日乘子法问题描述图
如"图2",f为曲面.c为平面, 黑色加粗线是f和c的交线.(约束就是限制自变量的变化范围).
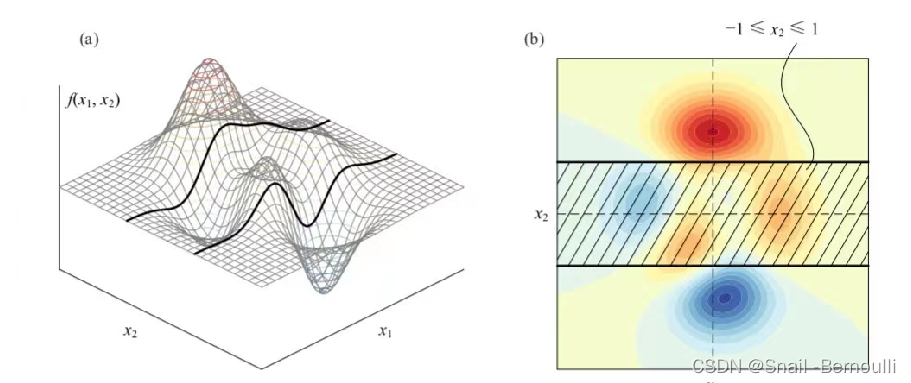
图2: 等式约束下的几何直观图与对应等值线图
2. 梯度共线
如图2,要使在c约束下,f取得最优解,则f的梯度(梯度是等值线的法向量, 如图3)与c的梯度(图中的红色箭头方向即为约束下的梯度方向, 如图4)共线.

图3: 等值线下梯度图
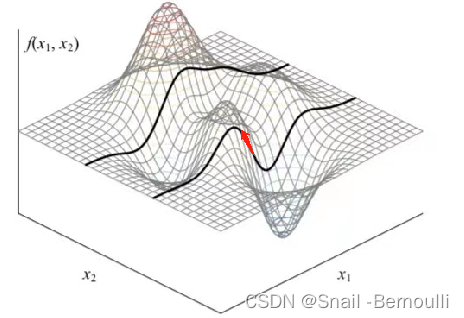
图4: c约束下f的梯度方向(共同方向.大小不重要)
梯度共线几何形式对应解析式如下:
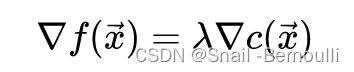
但是只有梯度共线并不能约束范围,因为向量可以平移不是. 故还需要确定范围.
3. 满足c = 0 约束
要在梯度共线的前提下,满足c





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








