SVM算法（深入理解拉格朗日乘子法与KKT条件的证明）

SVM应该是一个应用到数学知识很多的AI算法，涉及到大量线性代数的知识。

对偶关系、方向导数与梯度的关系、梯度方向与构造的可取区域的关系、拉格朗日乘子引入的真实含义等等。

（一）间隔与支持向量

SVM（support vector machine）支持向量机，最重要的就是在训练样本集中找到支持向量。

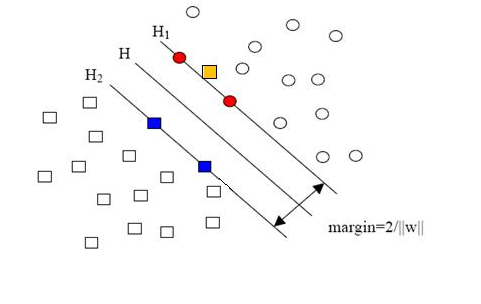
如图所示为最简单的二维平面上的分类，要想将圆圈一类和长方形一类分开需要找到一条直线，很显然这种直线不止一条，但是仿佛又存在一条直线能够让两类点到这条直线的距离取到一个最大值，那么我们是不是可以通过数学方法来求出这个值和这条分割线呢，答案是可以的。H1和H2这两条直线上的点就构成了支持向量（只需要这些点就可以求出分类直线），所以在最后的分类中，其余的点可有可无，当然也就不support啦！

（二）最大化间隔

推广到n维度，我们需要找到上图让margin=2/||w||最大的划分超平面。

也就是求解带约束的极值问题，将分割超平面设为为了方便求导，转换成下面等价问题：