PLA在Python下的简单实现
代码部分:(详细解释在代码中都有)
import numpy as np
from numpy import *
def pla():
W=np.ones(3)#初始化所有权重为1
count=0
# 这里定义x0到x2,其中公式证明出来x0衡等于1,不解释
# 自己构建六个可分割的二维坐标
dataset=[[1,0.107,0.643 ,1],
[1 ,0.241, 0.830 ,1],
[1 ,0.233 ,0.810, 1],
[1 ,0.361, 0.143, -1],
[1, 0.469, 0.321, -1],
[1, 0.859, 0.272, -1],
]
# 循环一次后如果有差错的点进入下一次循环
while True:
count+=1
iscompleted=True
# 采用视频所说的每一次循环所有的点,出现差错就改
fori in range(0,len(dataset)):
# x取到倒数第一个,然后最后一个作为y的值
X=dataset[i][:-1]
Y=np.dot(W,X)#矩阵相乘
# 计算出的结果和最后一个y值做对比
ifsign(Y)==sign(dataset[i][-1]):
continue
else:
iscompleted=False
# 如果出错的话,做后一个根据视频中公式w=w+yx
W=W+(dataset[i][-1])*np.array(X)
# 如果本次循环一个点都没有出错的话把最终权重输出
ifiscompleted:
break
print("final W is :",W)
print("count is :",count)
return W
w = pla()
数据部分的六个点为个人在二维坐标系上找到的六个可分割的点。在pla上跑一次之后得到的最终权重和训练轮数
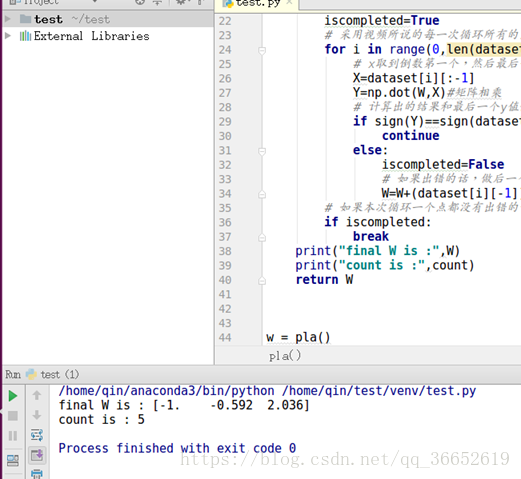
训练了五轮。





 本文介绍了一个简单的Python实现的感知器学习算法(PLA),通过六个预设的二维坐标点进行训练,最终输出了经过五轮迭代后的权重值。
本文介绍了一个简单的Python实现的感知器学习算法(PLA),通过六个预设的二维坐标点进行训练,最终输出了经过五轮迭代后的权重值。

















 656
656

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










